1214. Algorithm - BFS and DFSBFS and DFS
Use BSF and DSF to solve tree and graph problems.
1. BFS and DFS
Breadth-first search (BFS) is an algorithm for traversing or searching tree or graph data structures. It starts at the tree root (or some arbitrary node of a graph), and explores all of the neighbor nodes at the present depth prior to moving on to the nodes at the next depth level.
Depth-first search (DFS) is an algorithm for traversing or searching tree or graph data structures. The algorithm starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible along each branch before backtracking.
2. Tree Problems
A Tree is typically traversed in two ways:
- Breadth First Traversal (Or Level Order Traversal)
- Depth First Traversals
- Inorder Traversal (Left-Root-Right)
- Preorder Traversal (Root-Left-Right)
- Postorder Traversal (Left-Right-Root)
2.1 Binary Tree Level Order Traversal
Given a binary tree, return the level order traversal of its nodes’ values. (ie, from left to right, level by level).
For example:
Given binary tree [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
return its level order traversal as:
[
[3],
[9,20],
[15,7]
]
Implementation:
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> ans = new ArrayList<>();
if (root == null) {
return ans;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
List<Integer> list = new ArrayList<>();
int size = queue.size();
for (int i = 0; i < size; i++) {
TreeNode node = queue.poll();
list.add(node.val);
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
ans.add(list);
}
return ans;
}
2.2 Binary Tree Pre-Order Traversal
Given a binary tree, return the pre-order traversal of its nodes’ values.
For example:
Given binary tree [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
return its pre-order traversal as:
[3,9,20,15,7]
Implementation:
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> ans = new ArrayList<>();
if (root == null) {
return ans;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
ans.add(node.val);
if (node.right != null) {
stack.push(node.right);
}
if (node.left != null) {
stack.push(node.left);
}
}
return ans;
}
3. Graph Problems
3.1 All Paths From Source to Target
Given a directed, acyclic graph of N nodes. Find all possible paths from node 0 to node N-1, and return them in any order.
The graph is given as follows: the nodes are 0, 1, …, graph.length - 1. graph[i] is a list of all nodes j for which the edge (i, j) exists.
Example:
Input: [[1,2], [3], [3], []]
Output: [[0,1,3],[0,2,3]]
Explanation: The graph looks like this:
0--->1
| |
v v
2--->3
There are two paths: 0 -> 1 -> 3 and 0 -> 2 -> 3.
DFS Solution.
public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
List<List<Integer>> ans = new ArrayList<>();
List<Integer> list = new ArrayList<>();
list.add(0);
dfs(graph, 0, list, ans);
return ans;
}
private void dfs(int[][] graph, int node, List<Integer> list, List<List<Integer>> ans) {
if (node == graph.length - 1) {
ans.add(new ArrayList<>(list));
}
for (int nei : graph[node]) {
list.add(nei);
dfs(graph, nei, list, ans);
list.remove(list.size() - 1);
}
}
3.2 Traverse in Undirected Graph
Given an undirected graph with 5 vertices, traverse all vertices in this graph.
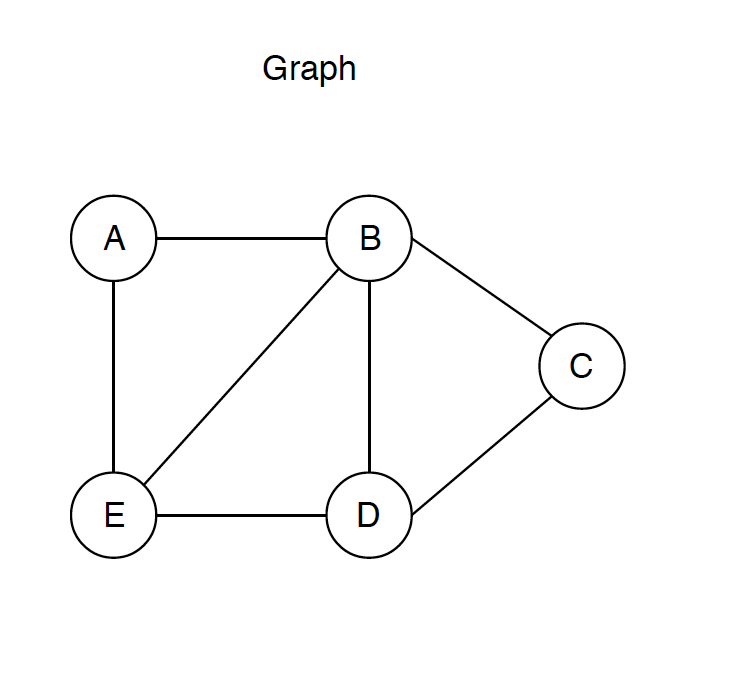
1) DFS Solution. DFS traverse returns [A, B, C, D, E].
// dfs, recursion
public void dfs(Node root, List<String> list) {
if (root == null) {
return;
}
list.add(root.name);
root.visited = true;
for (Node neighbor : root.neighbors) {
if (neighbor.visited == false) {
dfs(neighbor, list);
}
}
}
2) BFS Solution. BFS traverse returns [A, B, E, C, D].
public List<String> bfs(Node root) {
List<String> ans = new ArrayList<>();
if (root == null) {
return ans;
}
Queue<Node> queue = new LinkedList<Node>();
root.visited = true;
ans.add(root.name);
queue.offer(root);
while (!queue.isEmpty()) {
Node node = queue.poll();
for (Node neighbor : node.neighbors) {
if (neighbor.visited == false) {
neighbor.visited = true;
ans.add(neighbor.name);
queue.offer(neighbor);
}
}
}
return ans;
}
4. Matrix Problems
4.1 Number of Islands
Given a 2d grid map of ‘1’s (land) and ‘0’s (water), count the number of islands. An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.
Example 1:
Input:
11110
11010
11000
00000
Output: 1
Example 2:
Input:
11000
11000
00100
00011
Output: 3
4.2 Solution 1: DFS
Recursive. Modifying the original given grid, space: O(1), time: (m*n).
// DFS: change values of given grid, space: O(1), time: (m*n)
public int numIslands(char[][] grid) {
if (grid == null || grid.length == 0 || grid[0].length == 0) {
return 0;
}
int m = grid.length;
int n = grid[0].length;
int ans = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == '1') {
ans++;
dfs(grid, i, j);
}
}
}
return ans;
}
// set adjacent cell to 0
private void dfs(char[][] grid, int i, int j) {
int m = grid.length;
int n = grid[0].length;
if (i < 0 || i >= m || j < 0 || j >= n) {
return;
}
if (grid[i][j] == '1') {
grid[i][j] = '0';
dfs(grid, i - 1, j); // up
dfs(grid, i + 1, j); // down
dfs(grid, i, j - 1); // left
dfs(grid, i, j + 1); // right
}
}
4.3 Solution 2: BFS
Use queue to to store all cells for the next round scan. Use hashset to avoid adding duplicate cells to queue. Space: min(m,n), time: (m*n)
// BFS: change values of given grid, space: O(1), time: (m*n)
public int numIslands(char[][] grid) {
if (grid == null || grid.length == 0 || grid[0].length == 0) {
return 0;
}
int m = grid.length;
int n = grid[0].length;
int[] dr = new int[]{0, -1, 0, 1};
int[] dc = new int[]{1, 0, -1, 0};
int ans = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == '1') {
ans++;
Queue<int[]> queue = new LinkedList<>();
queue.offer(new int[] {i, j});
while (!queue.isEmpty()) {
Set<Integer> set = new HashSet<>();
int size = queue.size();
for (int k = 0; k < size; k++) {
int[] pos = queue.poll();
grid[pos[0]][pos[1]] = '0';
for (int p = 0; p < 4; p++) {
int r = pos[0] + dr[p];
int c = pos[1] + dc[p];
if (r < 0 || r >= m || c < 0 || c >= n || grid[r][c] == '0') {
continue;
}
if (!set.contains(r * n + c)) {
queue.offer(new int[] {r, c});
set.add(r * n + c);
}
}
}
}
}
}
}
return ans;
}
5. Classic Problems
- LeetCode 102 - Binary Tree Level Order Traversal
- LeetCode 144 - Binary Tree Preorder Traversal
- LeetCode 200 - Number of Islands
- LeetCode 542 - 01 Matrix
- LeetCode 797 - All Paths From Source to Target