1121. Data Structure - TreeTree and Binary Tree
Different types of tree data structure, tree traversal.
1. Tree
A tree is a data structure composed of nodes.The tree cannot contain cycles. The nodes may or may not be in a particular order, they could have any data type as values, and they may or may not have links back to their parent nodes.
1.1 Definition of Tree
- Each tree has a root node.
- The root node has zero or more child nodes.
- Each child node has zero or more child nodes, and so on.
1.2 Distinguishing the following Concepts
- Graphs vs. Trees: A tree is a connected graph without cycles.
- Trees vs.
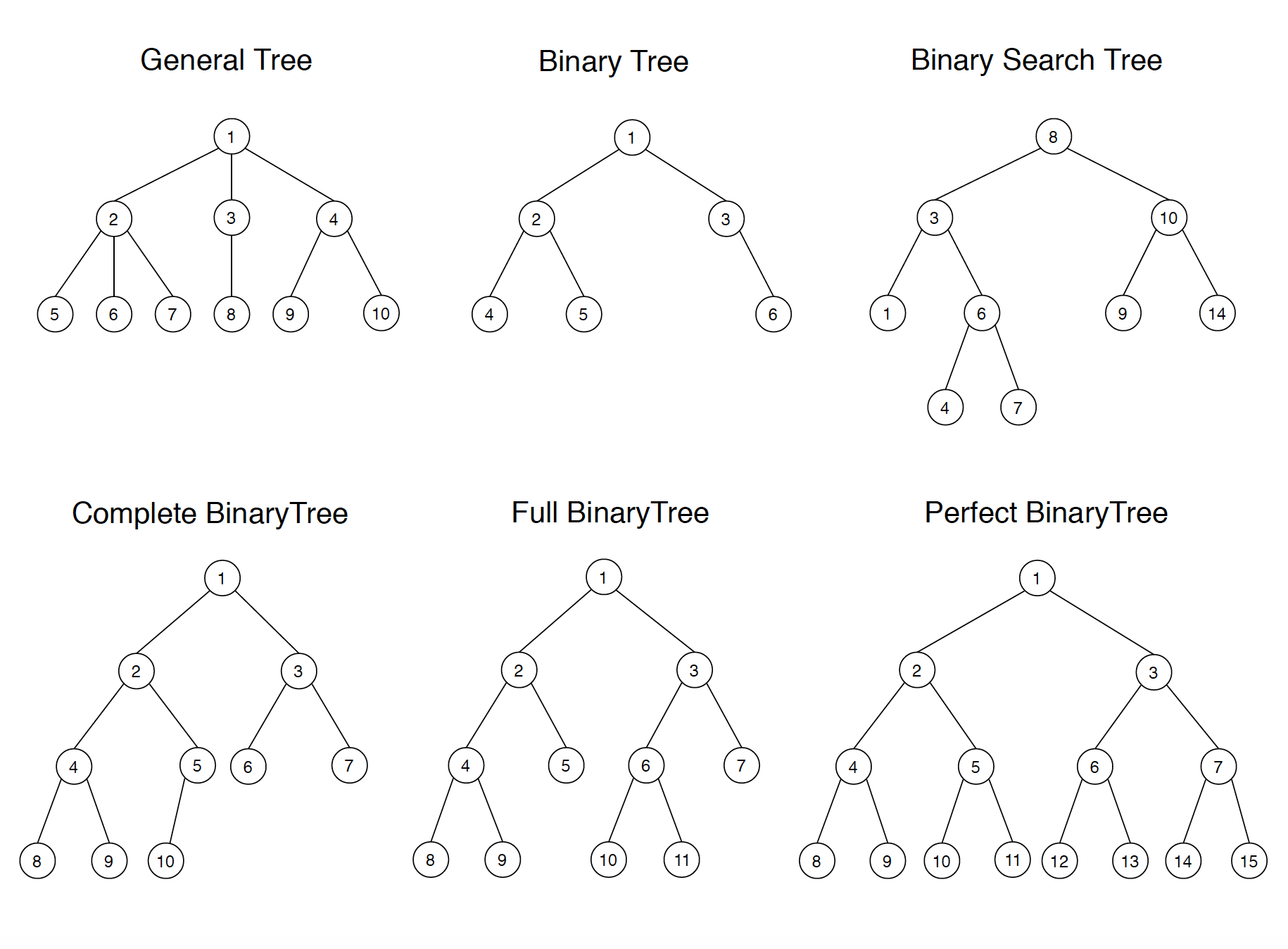
Binary Trees: Each node in binary tree has no more than 2 children nodes. - Binary Tree vs.
Binary Search Tree: Every node in BST fits a specific ordering property: all left descendents <= current node < all right descendents. Complete Binary Trees: A complete binary tree is a binary tree in which every level of the tree is fully filled, except for perhaps the last level. To the extent that the last level is filled, it is filled left to right.Full Binary Trees: A full binary tree is a binary tree in which every node has either zero or two children.That is, no nodes have only one child.Perfect Binary Trees: A perfect binary tree is one that is both full and complete. All leaf nodes will be at the same level, and this level has the maximum number of nodes.
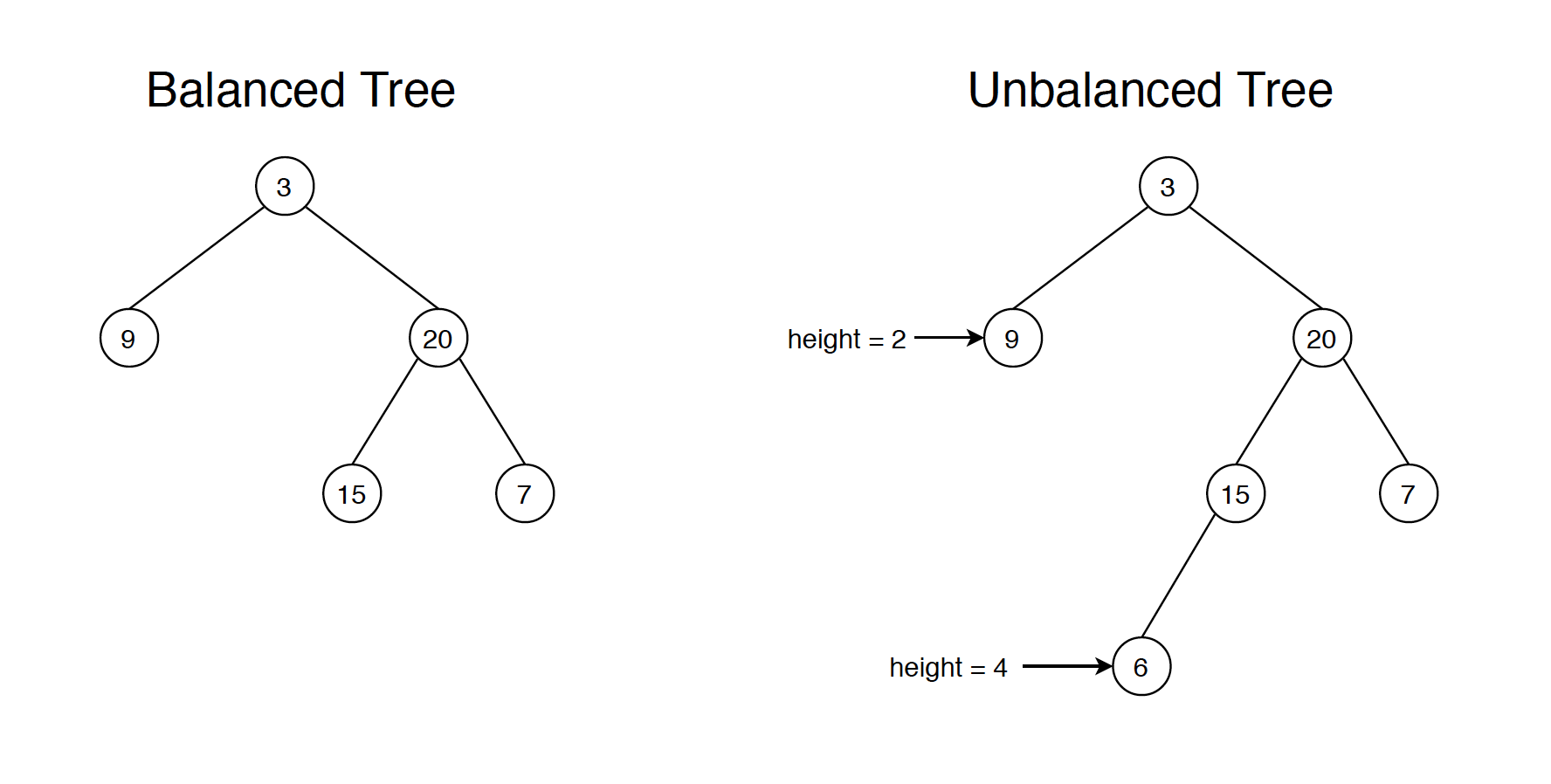
Balancedvs. Unbalanced: A tree is balanced if each sub-tree is balanced and the height of the two sub-trees differ by at most one.
1.3 Binary Tree Properties
- The maximum number of nodes at level
'l'of a binary tree is $2^{l-1}$. - Maximum number of nodes in a binary tree of height
'h'is $2^h-1$, since 1 + 2 + 4 + .. + $2^{h-1}$ = $2^h-1$. - In a Binary Tree with
'n'nodes, minimum possible height or minimum number of levels is $\log_{2}(n+1)$. - A Binary Tree with
'm'leaves has at least $\log_{2}(m) + 1$ levels. - In Binary tree where every node has 0 or 2 children, number of leaf nodes is always one more than nodes with two children.
2. Binary Tree Traversal
2.1 Definition of Binary Tree
A tree whose elements have at most 2 children is called a binary tree. Since each element in a binary tree can have only 2 children, we typically name them the left and right child.
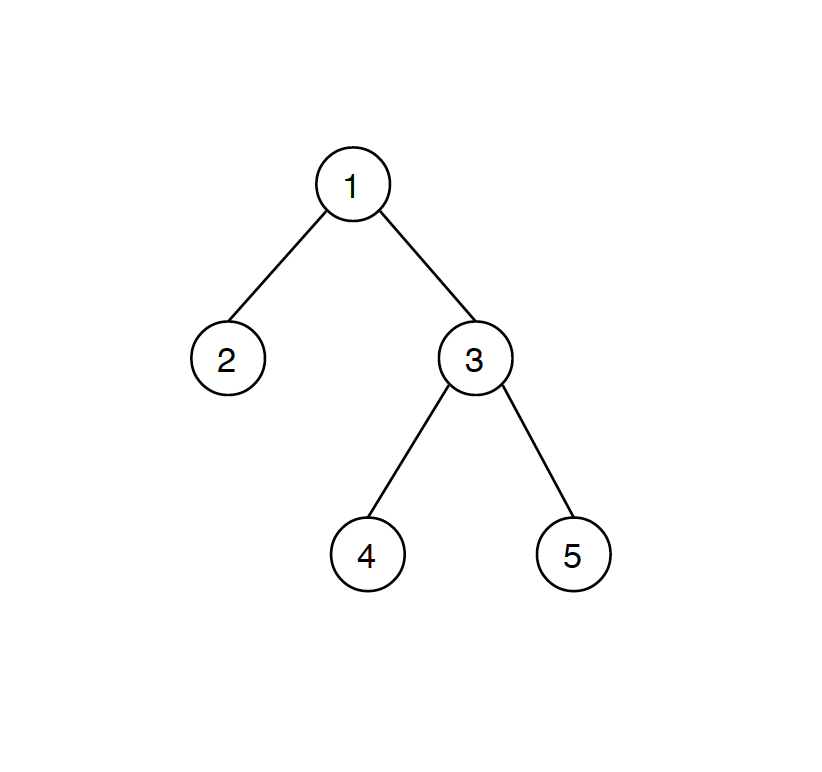
2.2 Implementing Tree Node
public class TreeNode {
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(int val) {
this.val = val;
this.left = null;
this.right = null;
}
}
2.3 Common Traversal Approaches On Binary Tree
1) Depth First Traversals:
- Preorder -> root, left child, right child
- Inorder -> left child, root, right child
- Postorder -> left child, right child, root
Implementation ways:
- Recursive
- Divide and Conquer
- Iterative
2) Breadth First Traversals:
- Level order traversal
Most of the tree traversal problems have the O(n) time complexity.
2.4 Implementation of Binary Tree Traversal - Recursive
Pre-Order: Given binary tree {1,2,3,#,#,4,5}, output [1,2,3,4,5].
// pre-order, recursive
public List<Integer> preorderRecursion(TreeNode root) {
List<Integer> list = new ArrayList<Integer>();
if (root == null) {
return list;
}
preorderHelper(root, list);
return list;
}
private void preorderHelper(TreeNode root, List<Integer> list) {
if (root == null) {
return;
}
list.add(root.val);
preorderHelper(root.left, res);
preorderHelper(root.right, res);
}
In-Order: Given binary tree {1,2,3,#,#,4,5}, output [2,1,4,3,5].
// in-order, recursive
public List<Integer> inorderRecursion(TreeNode root) {
List<Integer> list = new ArrayList<Integer>();
if (root == null) {
return list;
}
inorderHelper(root, list);
return list;
}
private void inorderHelper(TreeNode root, List<Integer> list) {
if (root == null) {
return;
}
inorderHelper(root.left, list);
res.add(root.val);
inorderHelper(root.right, list);
}
Post-Order: Given binary tree {1,2,3,#,#,4,5}, output [2,4,5,3,1].
// post-order, recursive
public List<Integer> postorderRecursion(TreeNode root) {
List<Integer> list = new ArrayList<Integer>();
if (root == null) {
return list;
}
postorderHelper(root, list);
return list;
}
private void postorderHelper(TreeNode root, List<Integer> list) {
if (root == null) {
return;
}
postorderHelper(root.left, list);
postorderHelper(root.right, list);
res.add(root.val);
}
2.5 Implementation of Binary Tree Traversal - Divide and Conquer
Pre-Order: Given binary tree {1,2,3,#,#,4,5}, output [1,2,3,4,5].
// pre-order, Divide Conquer
public List<Integer> preorderDivideConquer(TreeNode root) {
List<Integer> list = new ArrayList<Integer>();
if (root == null) {
return list;
}
// divide
List<Integer> left = preorderDivideConquer(root.left);
List<Integer> right = preorderDivideConquer(root.right);
// conquer
list.add(root.val);
list.addAll(left);
list.addAll(right);
return list;
}
In-Order: Given binary tree {1,2,3,#,#,4,5}, output [2,1,4,3,5].
// in-order, Divide Conquer
public List<Integer> inorderDivideConquer(TreeNode root) {
List<Integer> list = new ArrayList<Integer>();
if (root == null) {
return list;
}
// divide
List<Integer> left = inorderDivideConquer(root.left);
List<Integer> right = inorderDivideConquer(root.right);
// conquer
list.addAll(left);
list.add(root.val);
list.addAll(right);
return list;
}
Post-Order: Given binary tree {1,2,3,#,#,4,5}, output [2,4,5,3,1].
// post-order, Divide Conquer
public List<Integer> postorderDivideConquer(TreeNode root) {
List<Integer> list = new ArrayList<Integer>();
if(root == null) {
return list;
}
// divide
List<Integer> left = postorderDivideConquer(root.left);
List<Integer> right = postorderDivideConquer(root.right);
// conquer
list.addAll(left);
list.addAll(right);
list.add(root.val);
return list;
}
2.6 Implementation of Binary Tree Traversal - Iterative
Pre-Order: Given binary tree {1,2,3,#,#,4,5}, output [1,2,3,4,5].
// pre-order, traverse with stack
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
if (root == null) {
return list;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
list.add(node.val);
if (node.right != null) {
stack.push(node.right);
}
if (node.left != null) {
stack.push(node.left);
}
}
return list;
}
In-Order: Given binary tree {1,2,3,#,#,4,5}, output [2,1,4,3,5].
// in-order, traverse with stack
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
if (root == null) {
return list;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode curr = root;
while (curr != null || !stack.isEmpty()) {
while (curr != null) {
stack.push(curr);
curr = curr.left;
}
curr = stack.pop();
list.add(curr.val);
curr = curr.right;
}
return list;
}
Post-Order: Given binary tree {1,2,3,#,#,4,5}, output [2,4,5,3,1].
// post-order, traverse with stack
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<Integer>();
if (root == null) {
return list;
}
Stack<TreeNode> stack = new Stack<TreeNode>();
TreeNode curr = root;
while (curr != null || !stack.empty()) {
while (curr != null) {
stack.push(curr);
curr = curr.left;
}
curr = stack.peek();
if (curr.right == null) {
stack.pop();
list.add(curr.val);
curr = null;
} else {
TreeNode right = curr.right;
curr.right = null; // avoid being added to stack again.
curr = right;
}
}
return list;
}
2.7 Binary Tree Traversal(General Template)
Suppose we have a tree as follows.
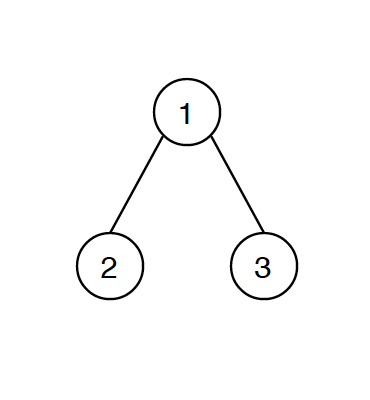 There are totally 6 traversal ways.
There are totally 6 traversal ways.
/**
* 1->2->3
*/
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
Deque<TreeNode> stack = new ArrayDeque<>();
TreeNode curr = root;
while(!stack.isEmpty() || curr != null) {
if(curr != null) {
stack.push(curr);
res.add(curr.val); // Add before going to children
curr = curr.left;
} else {
TreeNode node = stack.pop();
curr = node.right;
}
}
return res;
}
/**
* 2->1->3
*/
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
Deque<TreeNode> stack = new ArrayDeque<>();
TreeNode curr = root;
while(!stack.isEmpty() || curr != null) {
if(curr != null) {
stack.push(curr);
curr = curr.left;
} else {
TreeNode node = stack.pop();
res.add(node.val); // Add after all left children
curr = node.right;
}
}
return res;
}
/**
* 2->3->1
*/
public List<Integer> postorderTraversal(TreeNode root) {
LinkedList<Integer> res = new LinkedList<>();
Deque<TreeNode> stack = new ArrayDeque<>();
TreeNode curr = root;
while(!stack.isEmpty() || curr != null) {
if(curr != null) {
stack.push(curr);
res.addFirst(curr.val); // Reverse the process of preorder
curr = curr.right; // Reverse the process of preorder
} else {
TreeNode node = stack.pop();
curr = node.left; // Reverse the process of preorder
}
}
return res;
}
/**
* 1->3->2
*/
public List<Integer> preorderTraversal2(TreeNode root) {
List<Integer> res = new ArrayList<>();
Deque<TreeNode> stack = new ArrayDeque<>();
TreeNode curr = root;
while(!stack.isEmpty() || curr != null) {
if(curr != null) {
stack.push(curr);
res.add(curr.val); // Add before going to children
curr = curr.right;
} else {
TreeNode node = stack.pop();
curr = node.left;
}
}
return res;
}
/**
* 3->1->2
*/
public List<Integer> inorderTraversal2(TreeNode root) {
List<Integer> res = new ArrayList<>();
Deque<TreeNode> stack = new ArrayDeque<>();
TreeNode curr = root;
while(!stack.isEmpty() || curr != null) {
if(curr != null) {
stack.push(curr);
curr = curr.right;
} else {
TreeNode node = stack.pop();
res.add(node.val); // Add after all left children
curr = node.left;
}
}
return res;
}
/**
* 3->2->1
*/
public List<Integer> postorderTraversal2(TreeNode root) {
LinkedList<Integer> res = new LinkedList<>();
Deque<TreeNode> stack = new ArrayDeque<>();
TreeNode curr = root;
while(!stack.isEmpty() || curr != null) {
if(curr != null) {
stack.push(curr);
res.addFirst(curr.val); // Reverse the process of preorder
curr = curr.left; // Reverse the process of preorder
} else {
TreeNode node = stack.pop();
curr = node.right; // Reverse the process of preorder
}
}
return res;
}
2.8 Level-Order Traversal on Binary Tree
Given binary tree {3,9,20,#,#,15,7} as follows.
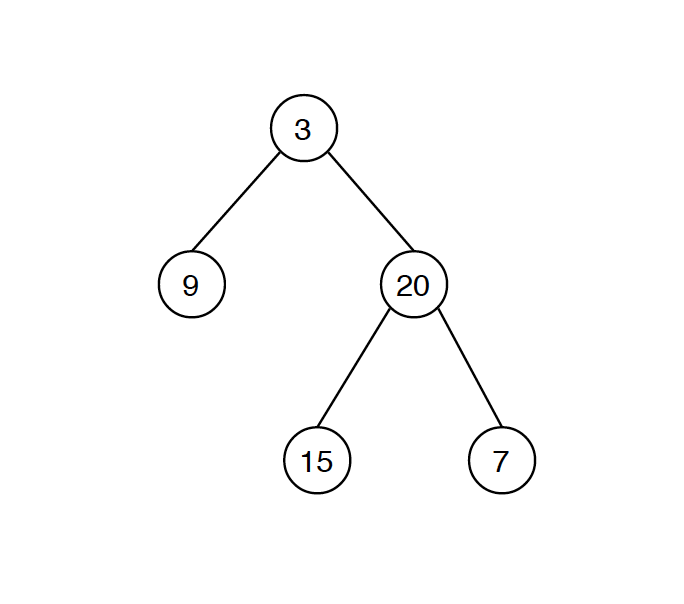 Return its level order traversal as below.
Return its level order traversal as below.
[
[3],
[9,20],
[15,7]
]
Approach 1: BSF: Use Queue to traverse the tree by layer.
/**
* @param root, the root node of a tree
* @return list of the values from the tree nodes in level order
*/
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<List<Integer>>();
if (root == null) {
return res;
}
Queue<TreeNode> queue = new LinkedList<TreeNode>();
queue.offer(root);
while (!queue.isEmpty()) {
List<Integer> level = new ArrayList<Integer>();
int size = queue.size();
for (int i = 0; i < size; i++) {
TreeNode node = queue.poll();
level.add(node.val);
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
res.add(level);
}
return res;
}
Approach 2: DFS: recursive
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> ans = new ArrayList<List<Integer>>();
helper(root, ans, 0);
return ans;
}
private void helper(TreeNode root, List<List<Integer>> list, int height) {
if (root == null) {
return;
}
if (height >= list.size()) {
list.add(new ArrayList<Integer>());
}
list.get(height).add(root.val);
helper(root.left, list, height + 1);
helper(root.right, list, height + 1);
}
3. Constructing Binary Tree
3.1 Serialization and Deserialization of Binary Tree
- Serialization - Convert a binary tree to string.
- Deserialization - Decode a string to binary tree.
For example, we have a tree as follows.
 Serialization will convert to tree to string [“1”,”2”,”3”,”#”,”#”,”4”,”5”] and deserialization will convert this string to the original tree.
Serialization will convert to tree to string [“1”,”2”,”3”,”#”,”#”,”4”,”5”] and deserialization will convert this string to the original tree.
Below is the implementation of serialization and deserialization in Java.
public class Codec {
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
if (root == null) {
return "";
}
Queue<TreeNode> queue = new LinkedList<TreeNode>();
queue.offer(root);
StringBuilder sb = new StringBuilder();
sb.append(root.val + ",");
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
TreeNode node = queue.poll();
if (node.left != null) {
queue.offer(node.left);
sb.append(node.left.val + ",");
} else {
sb.append("#,");
}
if (node.right != null) {
queue.offer(node.right);
sb.append(node.right.val + ",");
} else {
sb.append("#,");
}
}
}
sb.deleteCharAt(sb.length() - 1);
return sb.toString();
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
if (data == null || data.length() == 0) {
return null;
}
String[] values = data.split(",");
Queue<TreeNode> queue = new LinkedList<TreeNode>();
TreeNode root = new TreeNode(Integer.parseInt(values[0]));
queue.offer(root);
for (int i = 1; i < values.length; i = i + 2) {
TreeNode node = queue.poll();
if (!values[i].equals("#")) {
node.left = new TreeNode(Integer.parseInt(values[i]));
queue.offer(node.left);
}
if (!values[i + 1].equals("#")) {
node.right = new TreeNode(Integer.parseInt(values[i + 1]));
queue.offer(node.right);
}
}
return root;
}
}
3.2 Creating Tree With Level-Order String Array
For example, the below code create a tree with a root and right sub node. “#” stands for a empty node. The array contains level-order values for all the tree nodes.
TreeNode root = TreeNode.createInstance(new String[]{"1","#","3"});
Implementation of the ‘createInstance’ method.
public static TreeNode createInstance(String[] arr) {
if(arr == null || arr.length == 0) {
return null;
}
Queue<TreeNode> queue = new LinkedList<>();
TreeNode root = new TreeNode(Integer.parseInt(arr[0]));
queue.offer(root);
int index = 0;
while (index < arr.length - 1) {
TreeNode node = queue.poll();
if (node != null) {
String str = arr[++index];
if (!str.equals("#")) {
node.left = new TreeNode(Integer.parseInt(str));
queue.add(node.left);
}
str = arr[++index];
if (!str.equals("#")) {
node.right = new TreeNode(Integer.parseInt(str));
queue.add(node.right);
}
}
}
return root;
}