1123. Data Structure - Red Black Tree - draftRBT
Introduce red black tree and its properties.
1. Problems with Binary Search Tree
For Binary Search Tree, although the average time complexity for the search, insertion and deletion are all $O(\log{}n)$, where n is the number of nodes in the tree, the time complexity becomes to $O(n)$ in worst case - BST is not balanced.
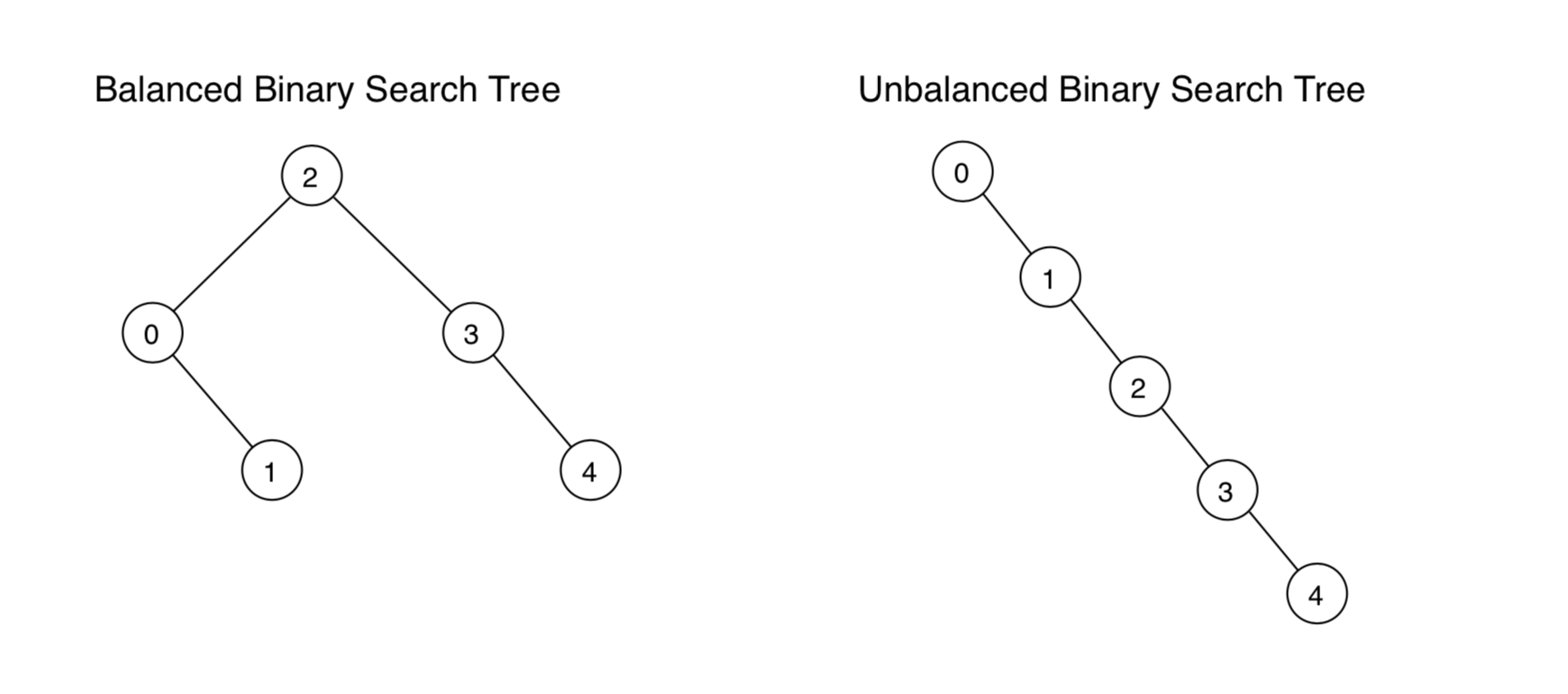
We can guarantee $O(\log{}n)$ time for all three operations by using a balanced tree - a tree that always has height log(n).
2. Red Black Tree
2.1 Definition of RBT
A red black tree is a binary search tree with following four properties.
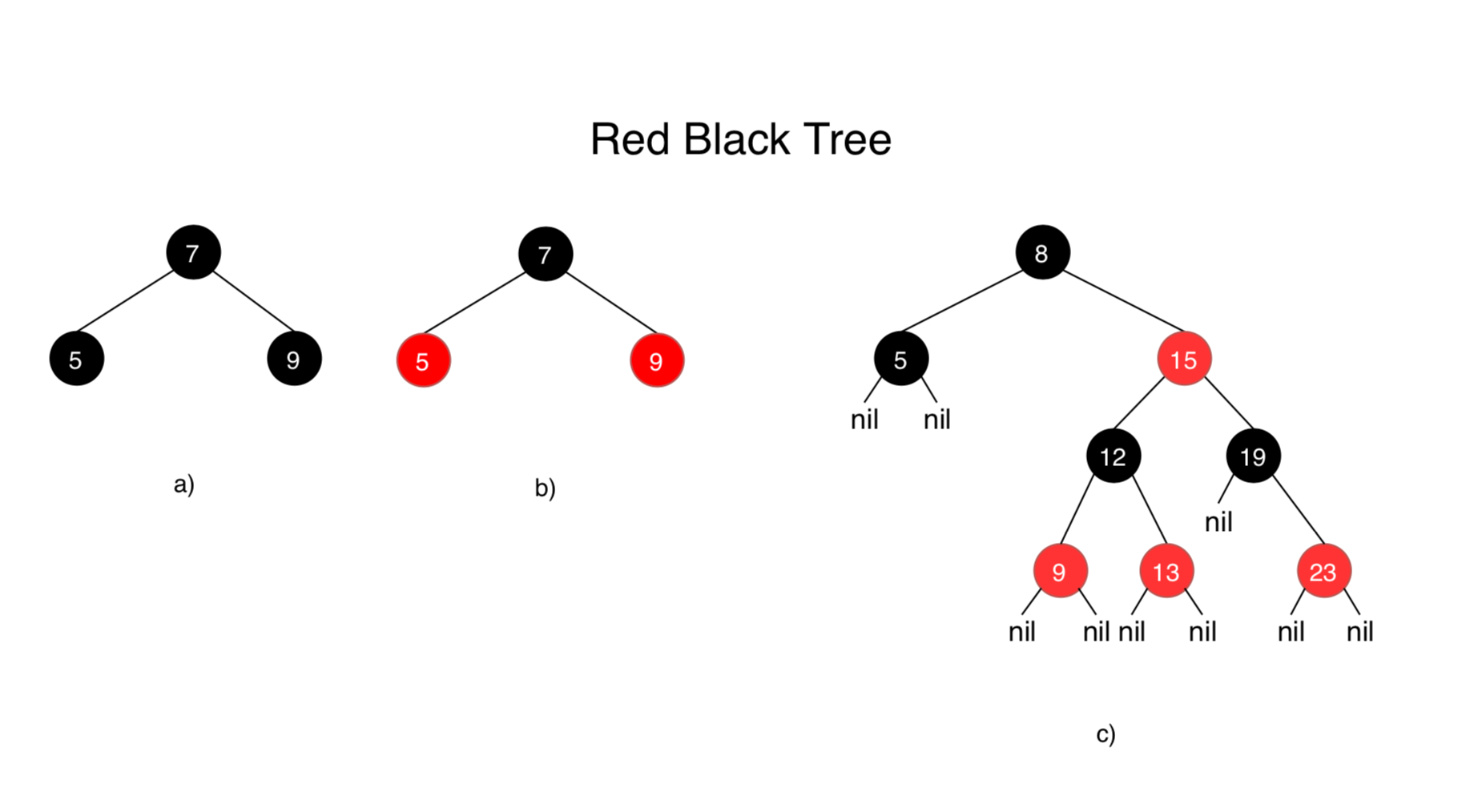
Color property: Each node has a color (red or black) associated with it (in addition to its key, left and right children).Root property: The root of the red-black tree is black.Red property: The children of a red node are black.Black property: For each node with at least one null child, the number of black nodes on the path from the root to the null child is the same.
Examples of Red Black Tree.
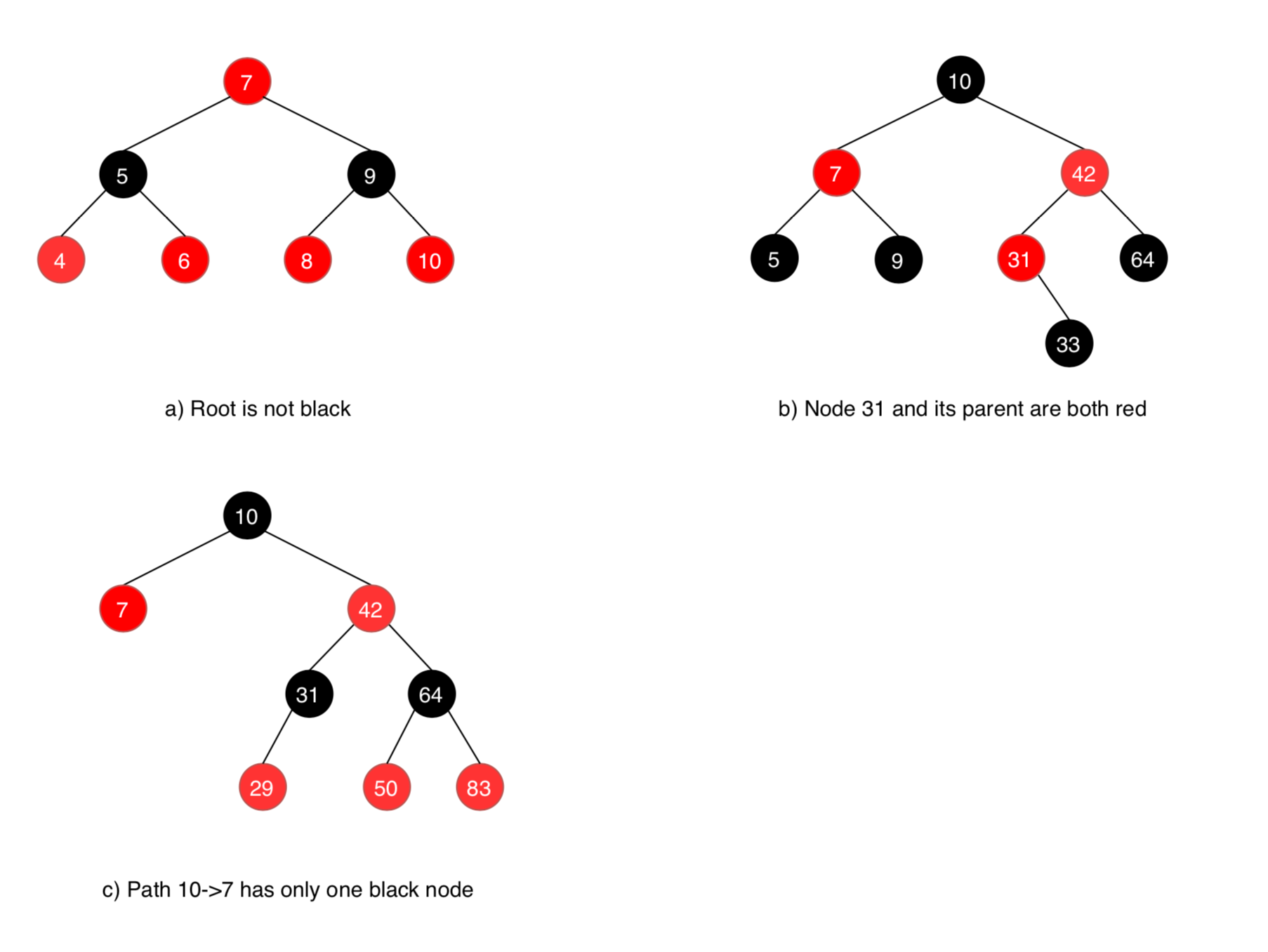
 The following examples are NOT Red Black Tree.
The following examples are NOT Red Black Tree.
1.2 Time Complexity
- Search - $O(\log{}n)$
- Insertion - $O(\log{}n)$
- Deletion - $O(\log{}n)$
1.3 Space Complexity
- $O(n)$
2. Search
Same as Binary Search Tree.
3. Insertion
The goal of the insert operation is to insert key x into tree T, and keep T’s red-black tree properties. We use Recoloring and Rotation to achieve that.
There are several cases when inserting a new key to RBT. We will go through all of them below.
3.1 Special Case: Empty Tree
A special case is required for an empty tree. If T is empty, replace it with a single black node containing x. This ensures that the root property is satisfied.
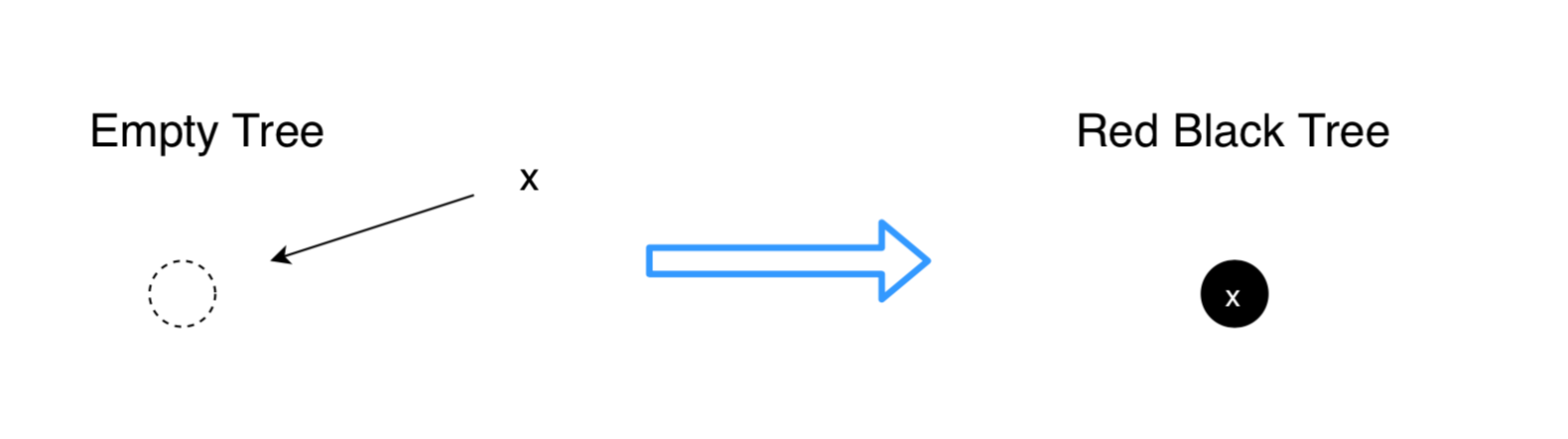
3.2 Non-empty Tree
If T is a non-empty tree, then we do the following:
- 1) Use the BST insert algorithm to add x to the tree
- 2) color the node containing x to red
- 3) restore red-black tree properties (if necessary)
For step 3, what we need to do depends on the color of x’s parent. Let p be x’s parent. We need to consider two cases:
- Case 1: x’s parent p is black. The insertion of x does not result in the red property being violated, so there’s nothing more to do.
- Case 2: K’s parent p is red.
For easy understanding, we have the following naming convention.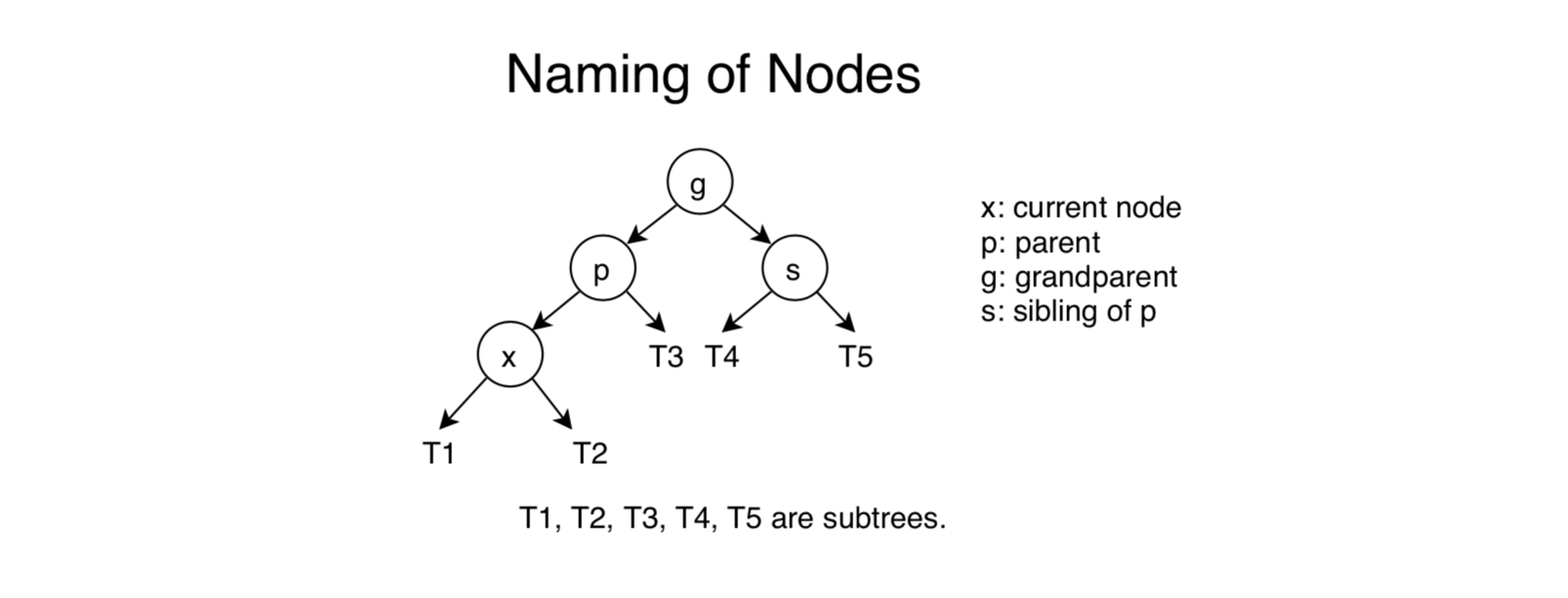 If
If pis red, then p now has a red child, which violates the red property. Note that p’s parent,g, must be black. In order to handle this double-red situation, we will need to consider the color of g’s other child, that is, p’s sibling,s. (Note that s might be null, i.e., g only has one child and that child is p.) We have two cases:- Case 2a:
p’s siblingsis red.
Perform recoloring ofp,sandg: the color ofpandsis changed to black and the color ofgis changed to red (unlessgis the root, in which case we leavegblack to preserve the root property).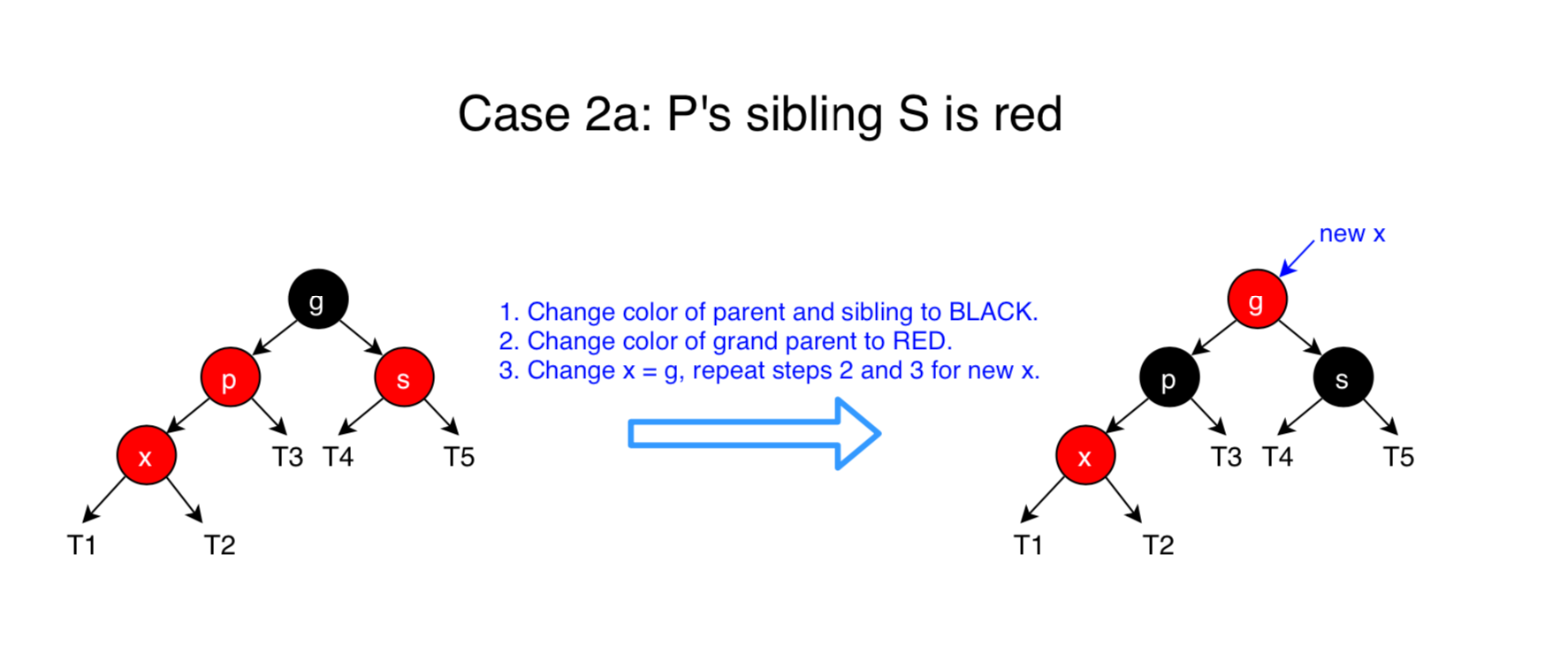 Recoloring does not affect the black property of a tree: the number of black nodes on any path that goes through
Recoloring does not affect the black property of a tree: the number of black nodes on any path that goes through pandgis unchanged whenpandgswitch colors (similarly forsandg). But, the recoloring may have introduced a double-red situation betweengandg’s parent. If that is the case, then werecursivelyhandle the double-red situation starting atgandg’s parent (instead ofxandx’s parent). - Case 2b:
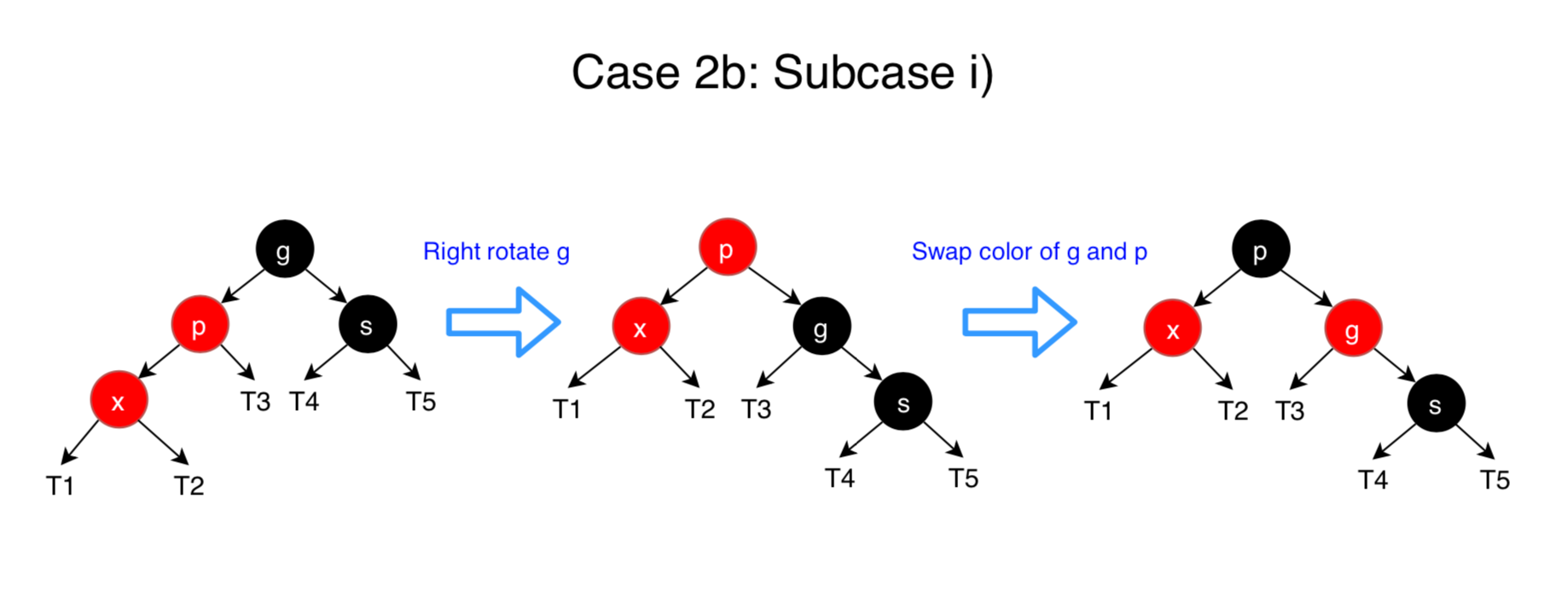
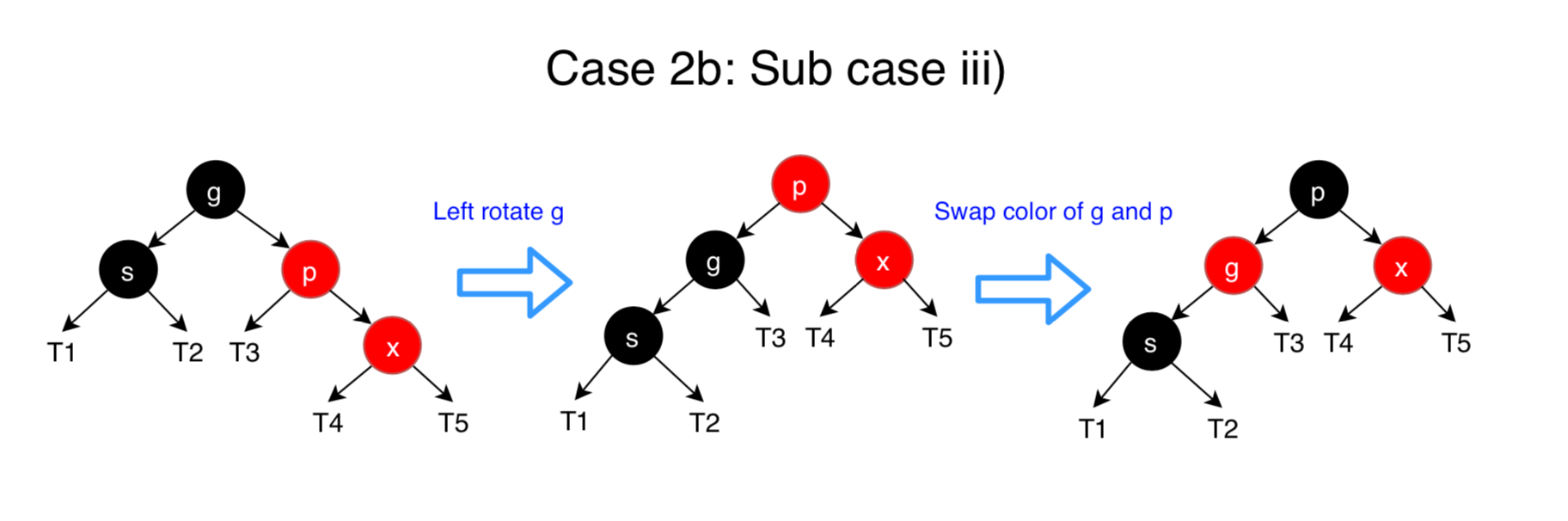
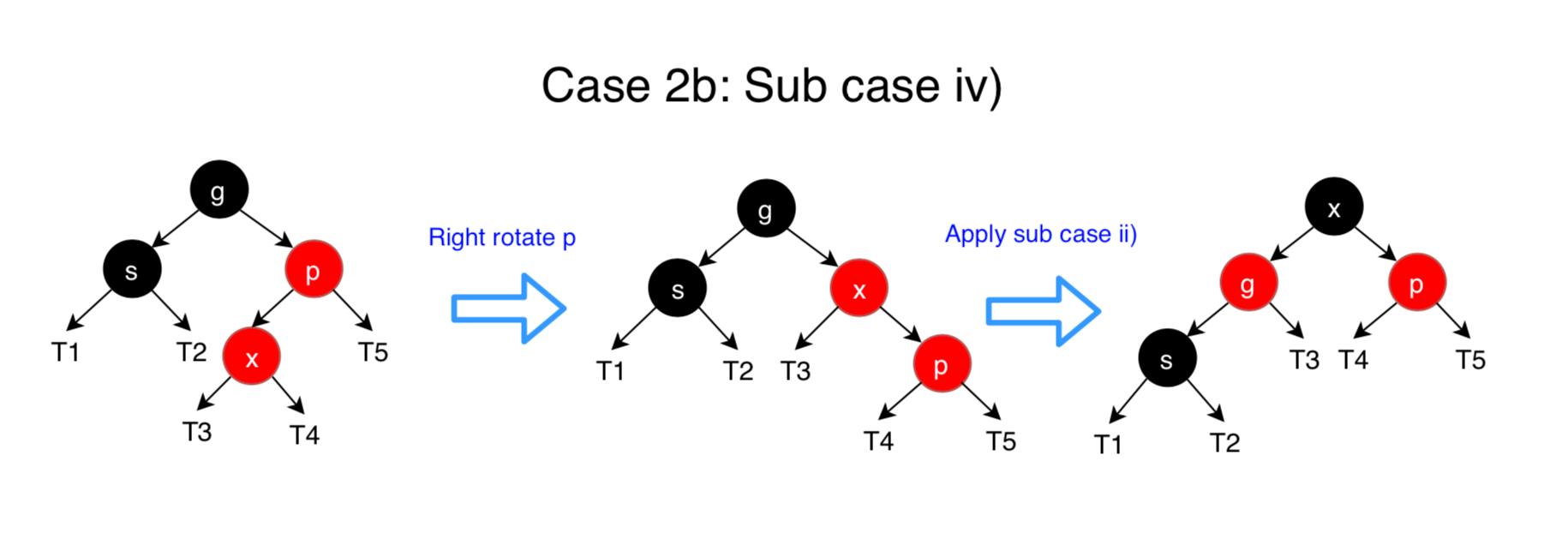
p’s siblingsis black or null.
Ifsis black or null, then we will do a tri-node restructuring ofx,pandg. There are four subcases for the relative ordering of x, p and g. The way a restructuring is done for each of the possibilities is shown below.- i) Left Left Case (p is left child of g and x is left child of p)
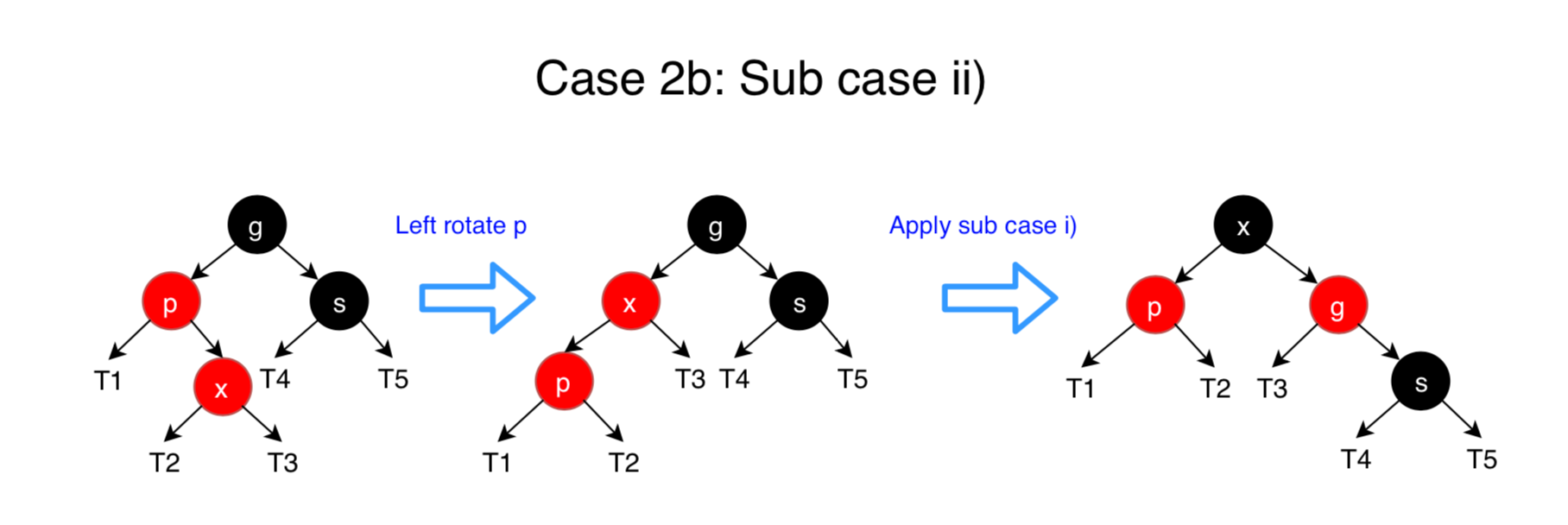
- ii) Left Right Case (p is left child of g and x is right child of p)
- iii) Right Right Case (Mirror of case i)
- iv) Right Left Case (Mirror of case ii)
- i) Left Left Case (p is left child of g and x is left child of p)
- Case 2a:
3.3 Example of Insertion
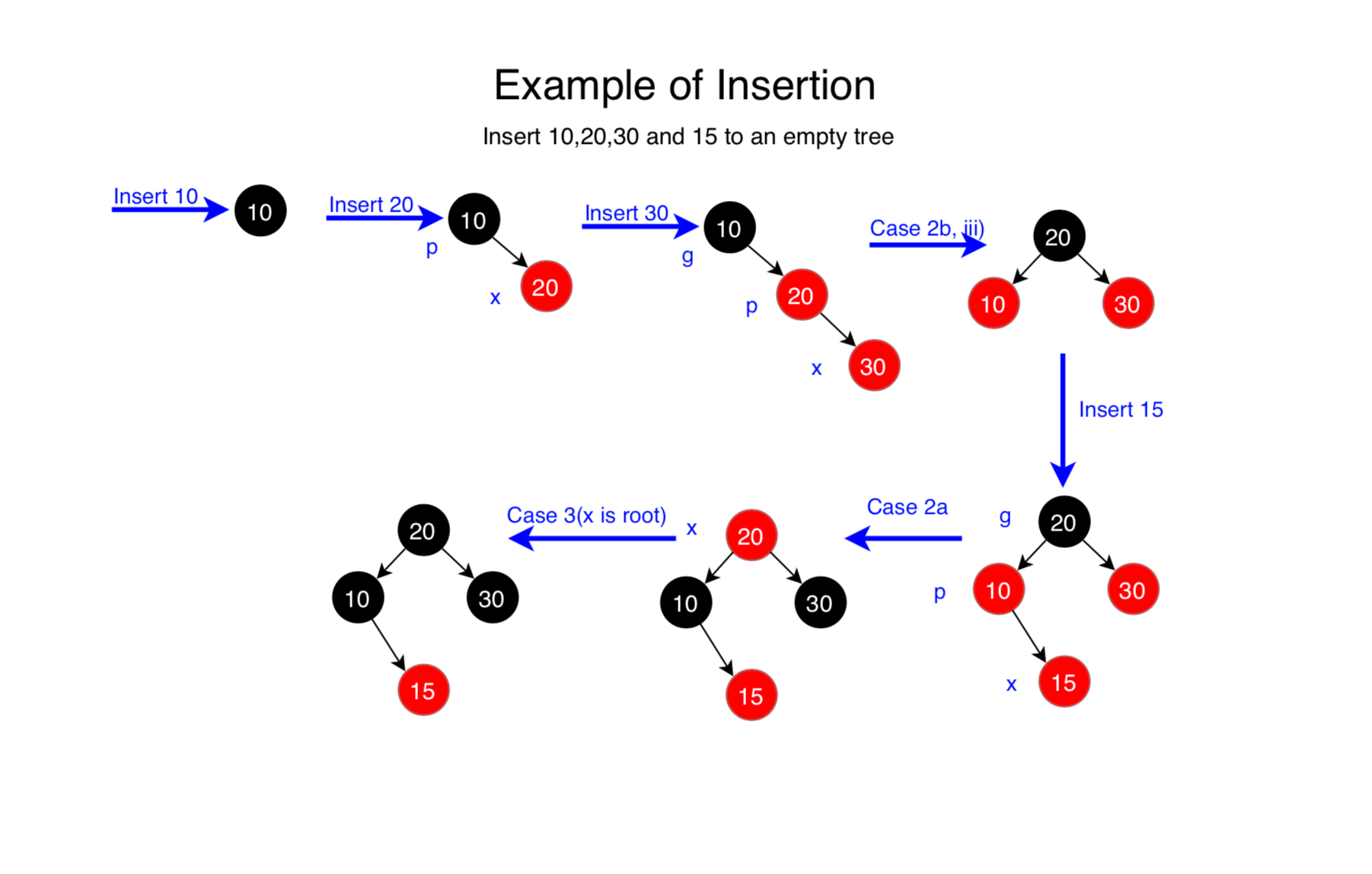
4. Deletion
There are three cases when deleting a node from Binary Search Tree.
- Node is leaf, has no children.
- Node has only one child.
- Node has two children.