1127. Data Structure - Segment TreeSegment Tree and Interval Tree
Implement segment tree for range search.
1. Segment Tree
Segment Tree (a.k.a Interval Tree) is an advanced data structure which can support queries like:
- which of these intervals contain a given point
- which of these points are in a given interval
1.1 The Range Search Question
1) What is the minimum number of array {4,-1,3,0,2}? The answer is -1.
2) What is the minimum number of this array within the range of index {2,3}? The answer is 0.
3) How to answer such question for any given range?
We have to create a matrix to store all the minimum values for all ranges. The matrix looks as follows.
| Index | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 4 | -1 | -1 | -1 | -1 |
| 1 | -1 | -1 | -1 | -1 | |
| 2 | 3 | 0 | 0 | ||
| 3 | 0 | 0 | |||
| 4 | 2 |
For example, to get the minimum number of range {2,4}, just find the cell {2,4}, which is 0.
Performance of Matrix Search:
- The space complexity is $O(n^2)$.
- The time complexity for building the matrix is $O(n^2)$, for searching is $O(1)$.
1.2 Solution with Segment Tree
The above question can be solved with Segment Tree as well. It has less storage and better performance.
- The space complexity is $O(n)$.
- The time complexity for building the tree is $O(n)$, for searching is $O(\log{}n)$.
Common Operations on Segment Tree:
- Build - $O(n)$
- Search - $O(\log{}n)$
- Modification - $O(\log{}n)$
2. Minimum Segment Tree
2.1 Definition of Minimum Segment Tree
The digram below shows what Minimum Segment Tree for given array {4,-1,3,0,2} looks like.
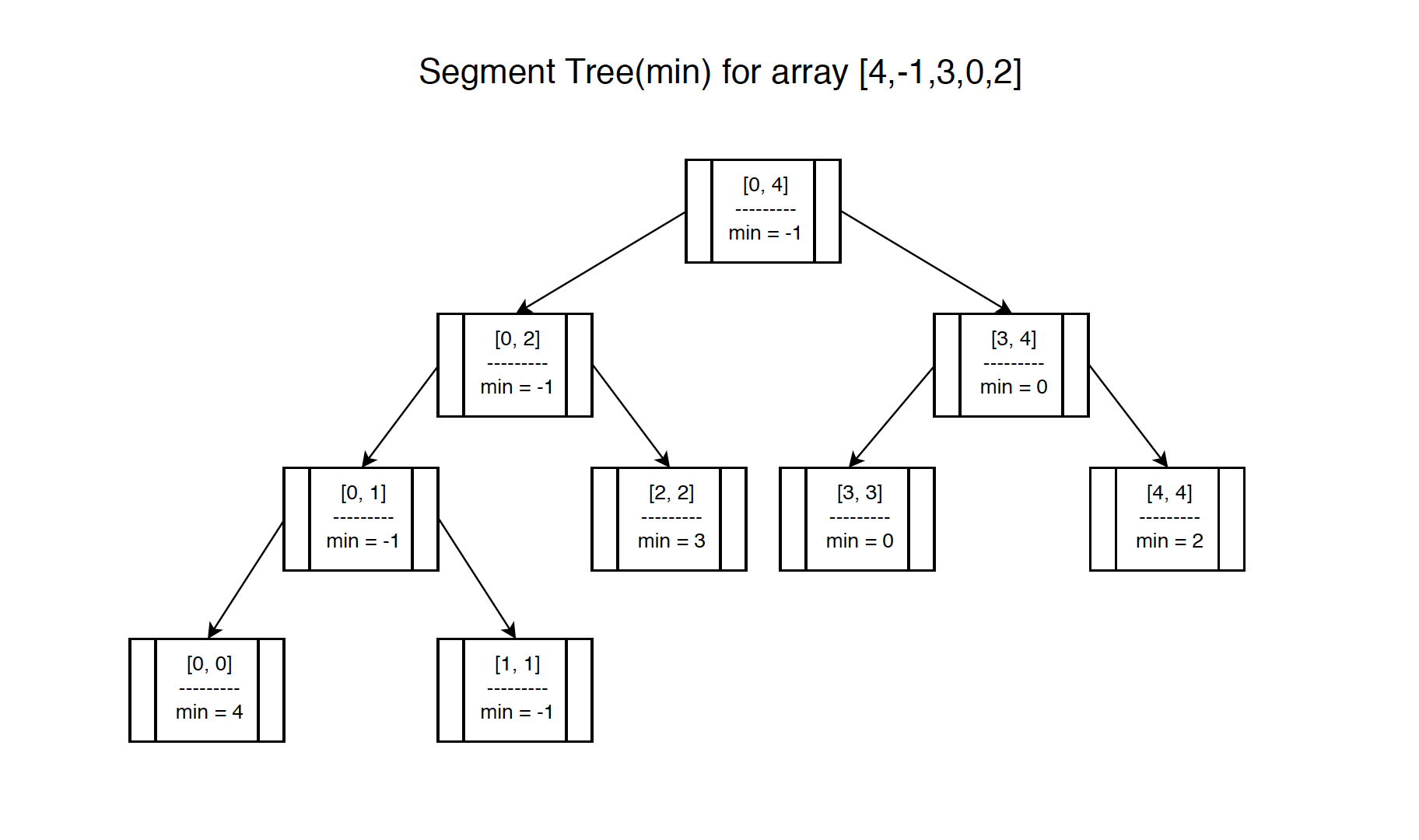
2.2 Creating Segment Tree Node
Create a class named SegmentTreeNode. Attributes start and end define the range. Attributes left and right are the children of the current node.
public class SegmentTreeNode {
public int start, end;
public int max, min, sum; // You can add other additional attributes
public SegmentTreeNode left, right;
public SegmentTreeNode(int start, int end) {
this.start = start;
this.end = end;
this.left = null;
this.right = null;
}
}
2.3 Constructing Minimum Segment Tree
Recursively construct the segment tree from top to bottom in binary approach. At each level, set the minimum value for the node.
private SegmentTreeNode build(int[] arr) {
if (arr == null || arr.length == 0) {
return null;
}
return buildMinHelpler(arr, 0, arr.length - 1);
}
private SegmentTreeNode buildMinHelpler(int[] arr, int start, int end) {
if (start > end) {
return null;
}
SegmentTreeNode root = new SegmentTreeNode(start, end);
if (start == end) {
root.min = arr[start];
return root;
}
int mid = start + (end - start) / 2;
root.left = buildMinHelpler(arr, start, mid);
root.right = buildMinHelpler(arr, mid + 1, end);
root.min = Math.min(root.left.min, root.right.min);
return root;
}
2.4 Searching on Minimum Segment Tree
There are four cases when searching with the given range.
- Search range is same with the range of root node, return the value directly.
- Search range is within the range of left child, continue searching in left node.
- Search range is within the range of right child, continue searching in right node.
- Search range crosses both left and right children, split the search and merge the result.
public int queryMin(int start, int end) {
return queryMin(this.root, start, end);
}
private int queryMin(SegmentTreeNode root, int start, int end) {
if (root == null) {
return 0;
}
// case 1: search range is same with the range of root node
if (root.start == start && root.end == end) {
return root.min;
}
int mid = root.start + (root.end - root.start) / 2;
// left range = [root.start, root.mid], right range = [root.mid + 1, root.end]
if (end <= mid) {
// case 2: search range is in the range of left child node
return queryMin(root.left, start, end);
} else if (start > mid) {
// case 3: search range is in the range of right child node
return queryMin(root.right, start, end);
} else {
//case 4: search range crosses both left and right children
int leftmin = queryMin(root.left, start, mid);
int rightmin = queryMin(root.right, mid + 1, end);
return Math.min(leftmin, rightmin);
}
}
3. Including Maximum and Sum
3.1 Definition of Minimum/Maximum/Sum Segment Tree
Actually, we can build Segment Tree for minimum, maximum and sum all at once.
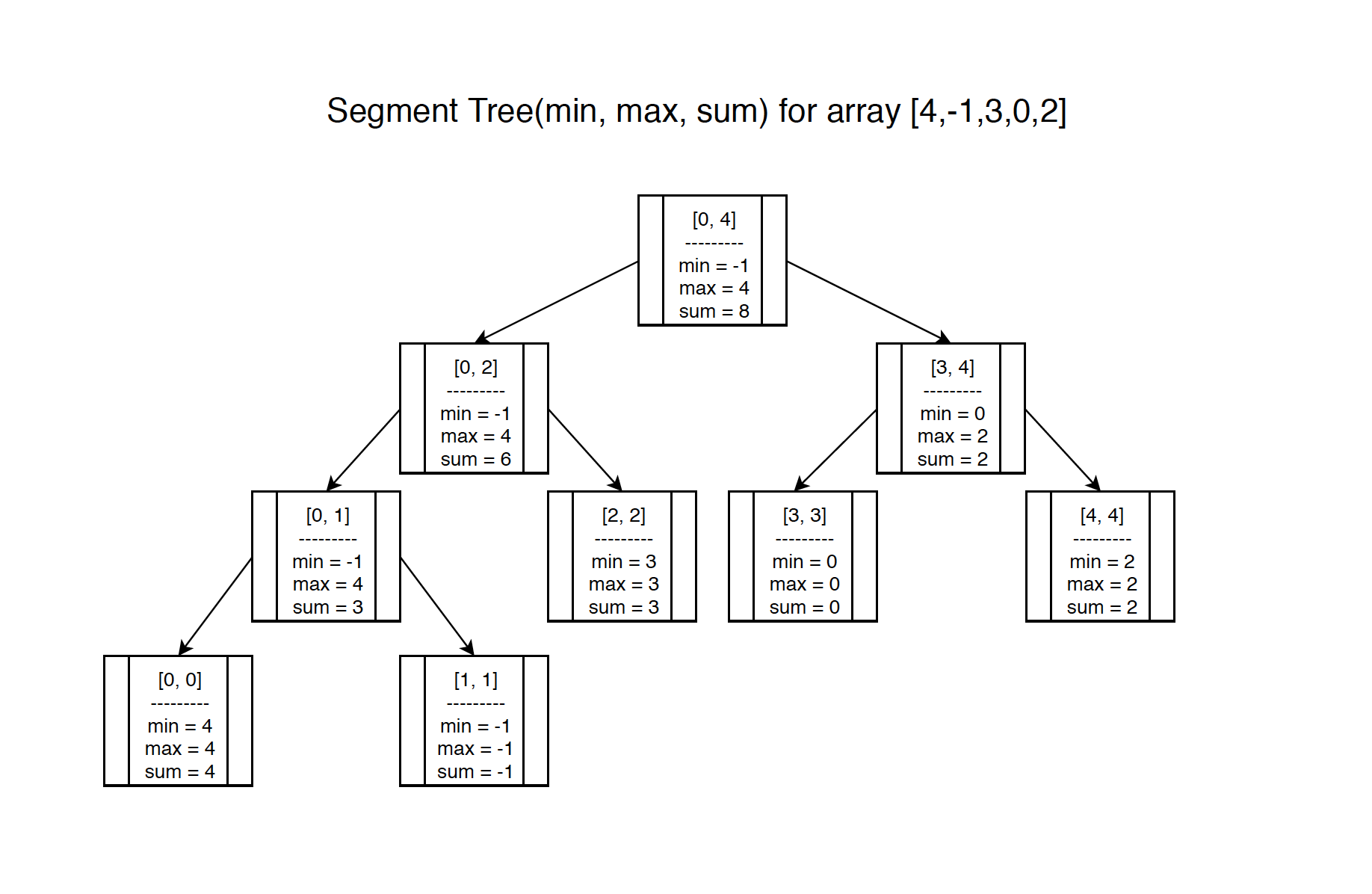
For each node, it contains min, max and sum value. Here are the samples for different ranges.
| Range | Min | Max | Sum |
|---|---|---|---|
| (0,4) | -1 | 4 | 8 |
| (2,3) | 0 | 3 | 3 |
| (0,1) | -1 | 4 | 3 |
| (1,4) | -1 | 3 | 4 |
3.2 Constructing Segment Tree
Refine the build method to include minimum, maximum and sum all together.
private SegmentTreeNode build(int[] arr) {
if (arr == null || arr.length == 0) {
return null;
}
return buildHelpler(arr, 0, arr.length - 1);
}
private SegmentTreeNode buildHelpler(int[] arr, int start, int end) {
if (start > end) {
return null;
}
SegmentTreeNode root = new SegmentTreeNode(start, end);
if (start == end) {
root.min = arr[start];
root.max = arr[start];
root.sum = arr[start];
return root;
}
int mid = start + (end - start) / 2;
root.left = buildHelpler(arr, start, mid);
root.right = buildHelpler(arr, mid + 1, end);
root.min = Math.min(root.left.min, root.right.min);
root.max = Math.max(root.left.max, root.right.max);
root.sum = root.left.sum + root.right.sum;
return root;
}
3.3 Searching on Segment Tree
Create three query methods named queryMin, queryMax and querySum. For the given segment tree and range, find the minimum value, maximum value and sum accordingly.
public int queryMin(int start, int end) {
return queryMin(this.root, start, end);
}
private int queryMin(SegmentTreeNode root, int start, int end) {
if (root == null) {
return 0;
}
// case 1: search range is same with the range of root node
if (root.start == start && root.end == end) {
return root.min;
}
int mid = root.start + (root.end - root.start) / 2;
if (end <= mid) {
// case 2: search range is in the range of left child node
return queryMin(root.left, start, end);
} else if (start > mid) {
// case 3: search range is in the range of right child node
return queryMin(root.right, start, end);
} else {
//case 4: search range crosses both left and right children
int leftmin = queryMin(root.left, start, mid);
int rightmin = queryMin(root.right, mid + 1, end);
return Math.min(leftmin, rightmin);
}
}
public int queryMax(int start, int end) {
return queryMax(this.root, start, end);
}
public int queryMax(SegmentTreeNode root, int start, int end) {
if (root == null) {
return 0;
}
// case 1: search range is same with the range of root node
if (root.start == start && root.end == end) {
return root.max;
}
int mid = root.start + (root.end - root.start) / 2;
if (end <= mid) {
// case 2: search range is in the range of left child node
return queryMax(root.left, start, end);
} else if (start > mid) {
// case 3: search range is in the range of right child node
return queryMax(root.right, start, end);
} else {
//case 4: search range crosses both left and right children
int leftmax = queryMax(root.left, start, mid);
int rightmax = queryMax(root.right, mid + 1, end);
return Math.max(leftmax, rightmax);
}
}
public int querySum(int start, int end) {
return querySum(this.root, start, end);
}
public int querySum(SegmentTreeNode root, int start, int end) {
if (root == null) {
return 0;
}
// case 1: search range is same with the range of root node
if (root.start == start && root.end == end) {
return root.sum;
}
int mid = root.start + (root.end - root.start) / 2;
if (end <= mid) {
// case 2: search range is in the range of left child node
return querySum(root.left, start, end);
} else if (start > mid) {
// case 3: search range is in the range of right child node
return querySum(root.right, start, end);
} else {
//case 4: search range crosses both left and right children
int leftsum = querySum(root.left, start, mid);
int rightsum = querySum(root.right, mid + 1, end);
return leftsum + rightsum;
}
}
4. Modification
4.1 Minimum Segment Tree
If value on leaf node is changed, we need to update its parent accordingly. For example, if we change the value of the second leaf from ‘-1’ to ‘5’ in minimum segment tree, then all nodes from root to this leaf need to be updated.
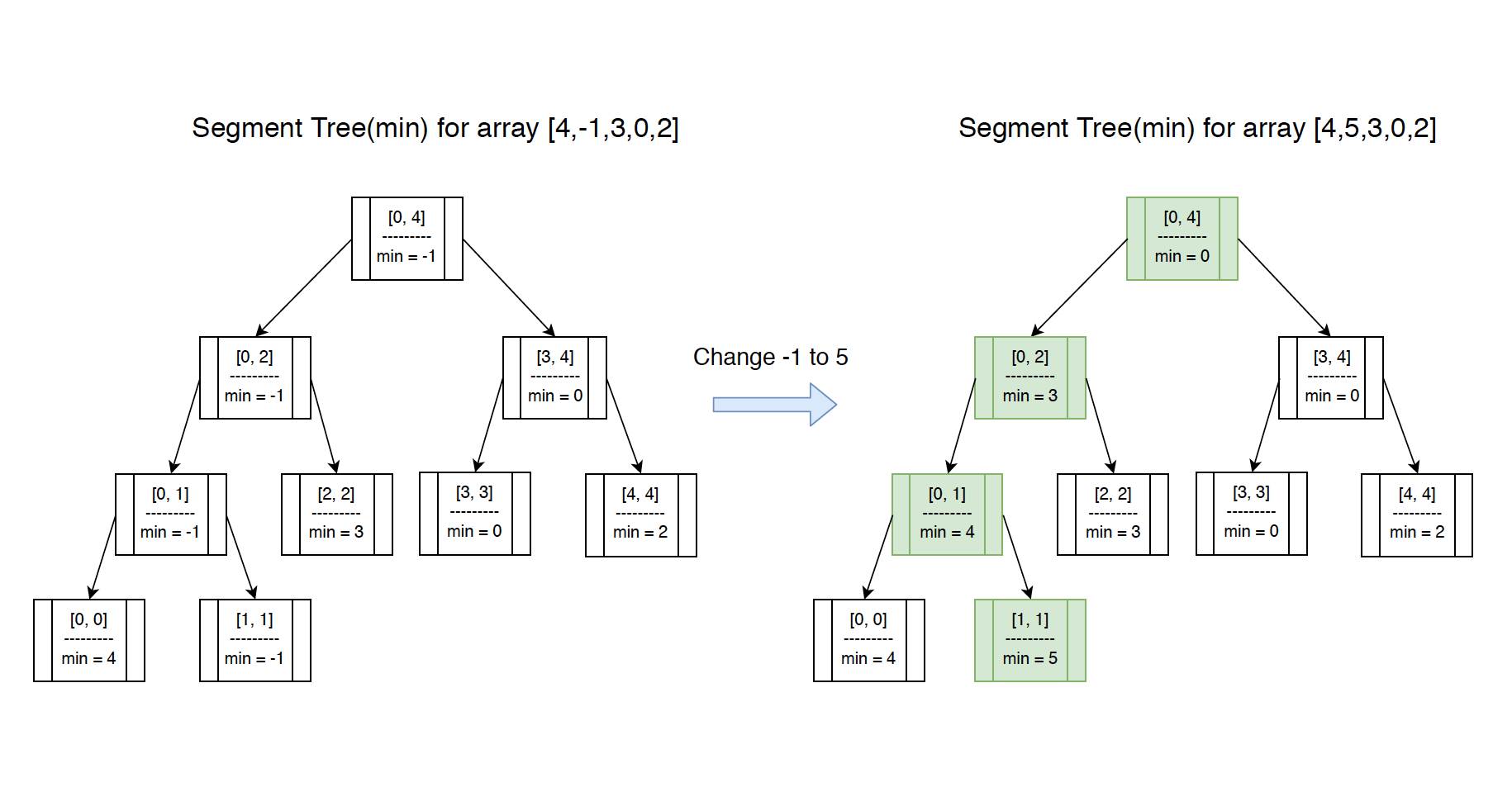
The implementation of the modify method.
public void modify(int index, int value) {
modify(this.root, index, value);
}
private void modify(SegmentTreeNode root, int index, int value) {
if (root == null) {
return;
}
if (root.start == root.end && root.start == index) {
root.min = value;
return;
}
int mid = root.start + (root.end - root.start) / 2;
if (index <= mid) {
modify(root.left, index, value);
} else {
modify(root.right, index, value);
}
root.min = Math.min(root.left.min, root.right.min);
}
4.2 Modifying Maximum and Sum
Similarly, if we change the value, the max value and the sum value will be affected as well.
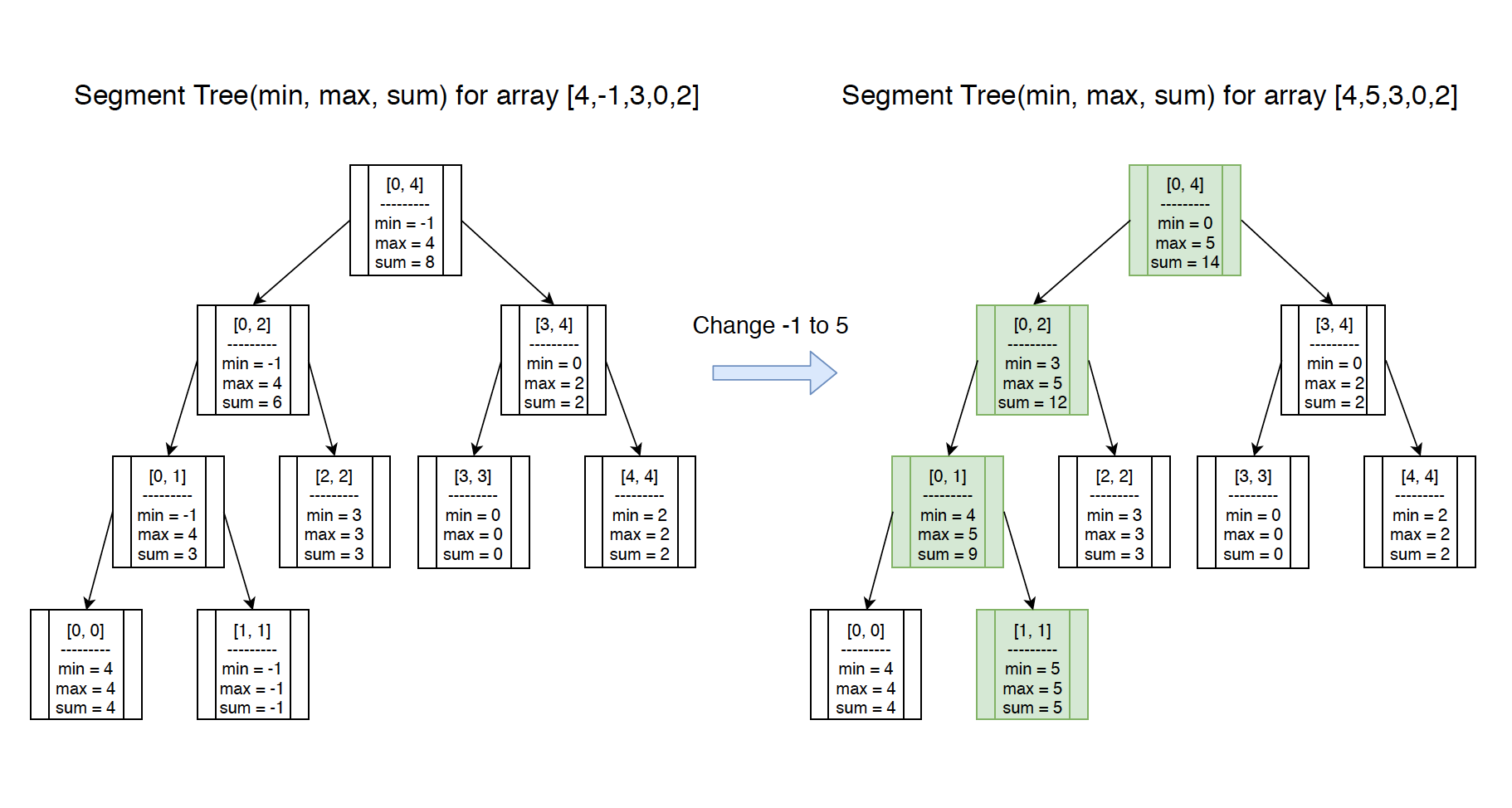 Refine the
Refine the modify method to update the max value and the sum value together.
public void modify(int index, int value) {
modify(this.root, index, value);
}
private void modify(SegmentTreeNode root, int index, int value) {
if (root == null) {
return;
}
if (root.start == root.end && root.start == index) {
root.min = value;
root.max = value;
root.sum = value;
return;
}
int mid = root.start + (root.end - root.start) / 2;
if (index <= mid) {
modify(root.left, index, value);
} else {
modify(root.right, index, value);
}
root.min = Math.min(root.left.min, root.right.min);
root.max = Math.max(root.left.max, root.right.max);
root.sum = root.left.sum + root.right.sum;
}
5. Classic Problems
- LintCode 201 - Segment Tree Build
- LintCode 202 - Segment Tree Query
- LintCode 203 - Segment Tree Modify
- LintCode 205 - Interval Minimum Number
- LintCode 206 - Interval Sum
- LintCode 207 - Interval Sum II
- LintCode 248 - Count of Smaller Number
- LintCode 249 - Count of Smaller Number before itself