1111. Data Structure - Linked ListSingly Linked List and Doubly Linked List
Implement linked list.
1. Linked List
A linked list is represented by a sequence of nodes. Each node contains a link to another node. There are two main types of linked list.
- Singly Linked List - Each node has only one link, points to the next node.
- Doubly Linked List - Each node has two links, one points to previous node, another points to the next node.
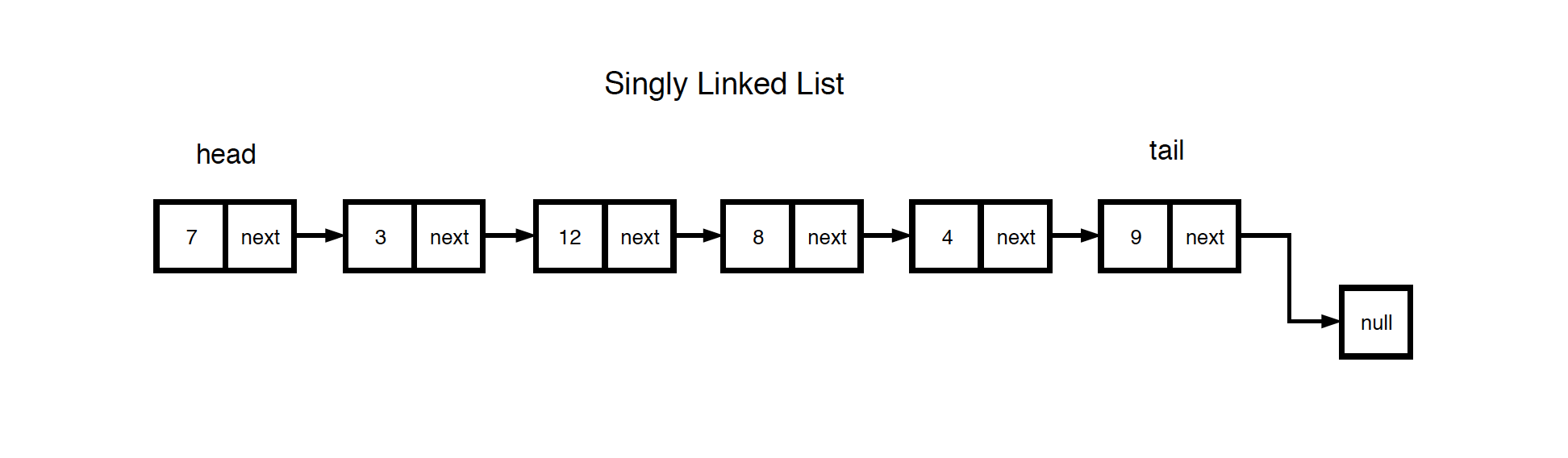
1.1 Singly Linked List
Each node has an attribute to represent its value. It also has one pointer, linking it to the next node in the linked list.
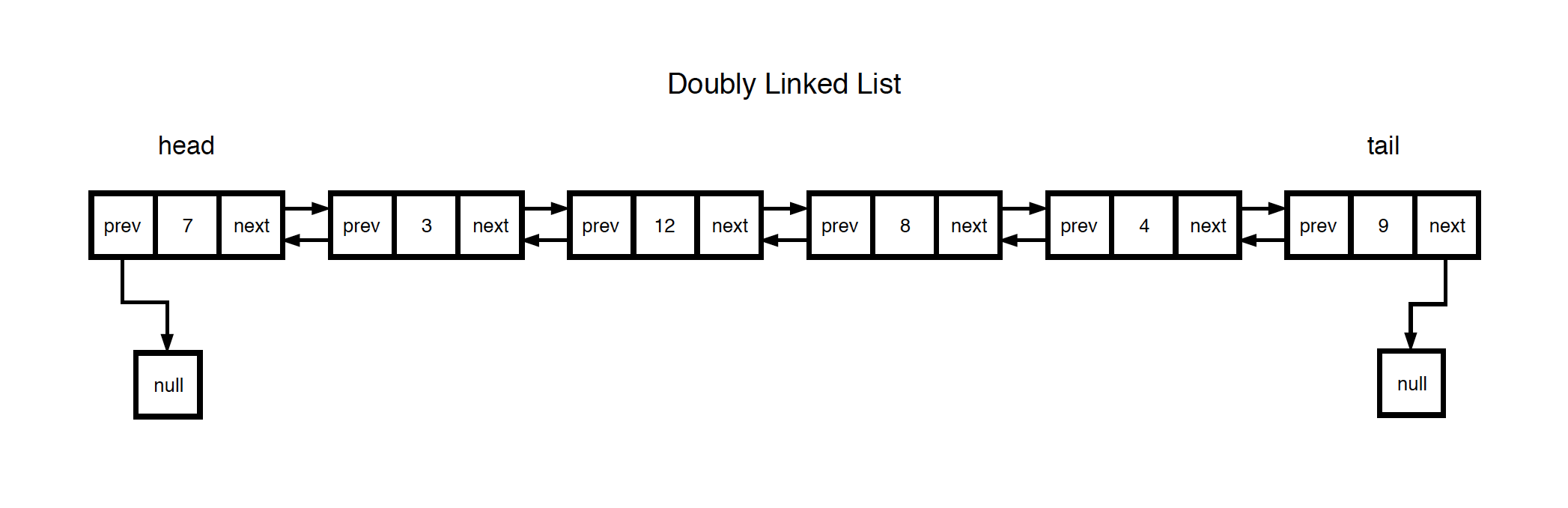
1.2 Doubly Linked List
Each node has an attribute to represent its value. Meanwhile, it has two pointers, the first pointer links to the next node, and the second pointer links to the previous node.
2. Implementation
2.1 Creating Singly Linked List
First, define the structure of SinglyLinkedNode. Each node has an attribute val, storing the value of the node. And it also has one pointer next, storing the address of the next node.
public class SinglyLinkedNode {
public int val;
public SinglyLinkedNode next;
public SinglyLinkedNode(int val) {
this.val = val;
this.next = null;
}
}
Next, create a class named SinglyLinkedList with one static method create. This method reads values from an array and constructs a list with SinglyLinkedNode. Be aware of the fact that, for the last node, its next is always NULL.
public class SinglyLinkedList {
// create a singly linked list with the given array
public static SinglyLinkedNode create(int[] arr) {
if (arr == null || arr.length == 0) {
return null;
}
SinglyLinkedNode dummy = new SinglyLinkedNode(0);
SinglyLinkedNode curr = dummy;
for (int i = 0; i < arr.length; i++) {
curr.next = new SinglyLinkedNode(arr[i]);
curr = curr.next;
}
return dummy.next;
}
}
2.2 Creating Doubly Linked List
First, define the structure of DoublyLinkedNode. Each node has an attribute val, storing the value of the node. And it has two pointers previous and next, storing the addresses of the previous node and the next node.
public class DoublyLinkedNode {
public int val;
public DoublyLinkedNode previous;
public DoublyLinkedNode next;
public DoublyLinkedNode(int val) {
this.val = val;
this.previous = null;
this.next = null;
}
}
Next, create a class named DoublyLinkedList with one static method create. This method reads values from an array and constructs a list with DoublyLinkedNode. During creation of DoublyLinkedNode, set its previous and next accordingly.
public class DoublyLinkedList {
// create a doubly linked list with the given array
public static DoublyLinkedNode create(int[] arr) {
if (arr == null || arr.length == 0) {
return null;
}
DoublyLinkedNode dummy = new DoublyLinkedNode(0);
DoublyLinkedNode curr = dummy;
for (int i = 0; i < arr.length; i++) {
curr.next = new DoublyLinkedNode(arr[i]);
curr.next.previous = curr;
curr = curr.next;
}
return dummy.next;
}
}
3. Common Operations
Here are some basic approaches for solving linked list problems.
- Dummy Node
- Reversing Linked List
- Fast and Slow Pointers
- Find middle node
All below questions/codes are based on singly linked list.
3.1 Reversing Linked List
Reverse a linked list and return the head of the new reversed list.
/**
* @param head of the original linked list
* @return reversed linked list
*
* Sample
* Input: 7->3->12->8->4->9
* Output: 9->4->8->12->3->7
*
*/
public ListNode reverse(ListNode head) {
ListNode prev = null;
while (head != null) {
ListNode next = head.next;
head.next = prev;
prev = head;
head = next;
}
return prev;
}
3.2 Finding the Middle Node in Linked List
Find the middle node of the given linked list and return it.
/**
* @param head of the original linked list
* @return middle node of the linked list
*
* Sample
* Input: 7->3->12->8->4
* Output: 12
* Input: 7->3->12->8->4->9
* Output: 12
*
*/
public ListNode findMiddle(ListNode head) {
if (head == null) {
return null;
}
// define fast and slow pointers
ListNode fast = head.next;
ListNode slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next; // two steps for each pace
slow = slow.next; // one step for each pace
}
return slow;
}
3.3 Detecting Cycle in Linked List
Check whether there is any cycle exists in a given linked list. The below approach adapts the Floyd's Cycle Detection Algorithm, Tortoise & Hare or two pointers.
/**
* @param head of the original linked list
* @return middle node of the linked list
*
* Sample
* Input: 7->3->12->8->4->9
* Output: false
* Input: 7->3->12->8->4->9->12
* Output: true (12->8->4->9->12 is the loop)
*
*/
public boolean hasCycle(ListNode head) {
if (head == null || head.next == null) {
return false;
}
ListNode fast = head.next; // or ListNode fast = head.next
ListNode slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) {
return true;
}
}
return false;
}
3.4 Finding the Node Where Cycle Begins
Find the node where cycle begins in a given linked list. If there is no cycle, return null.
We use the following figure to illustrate the solution. We will use the fast pointer and the slow pointer to solve this problem.
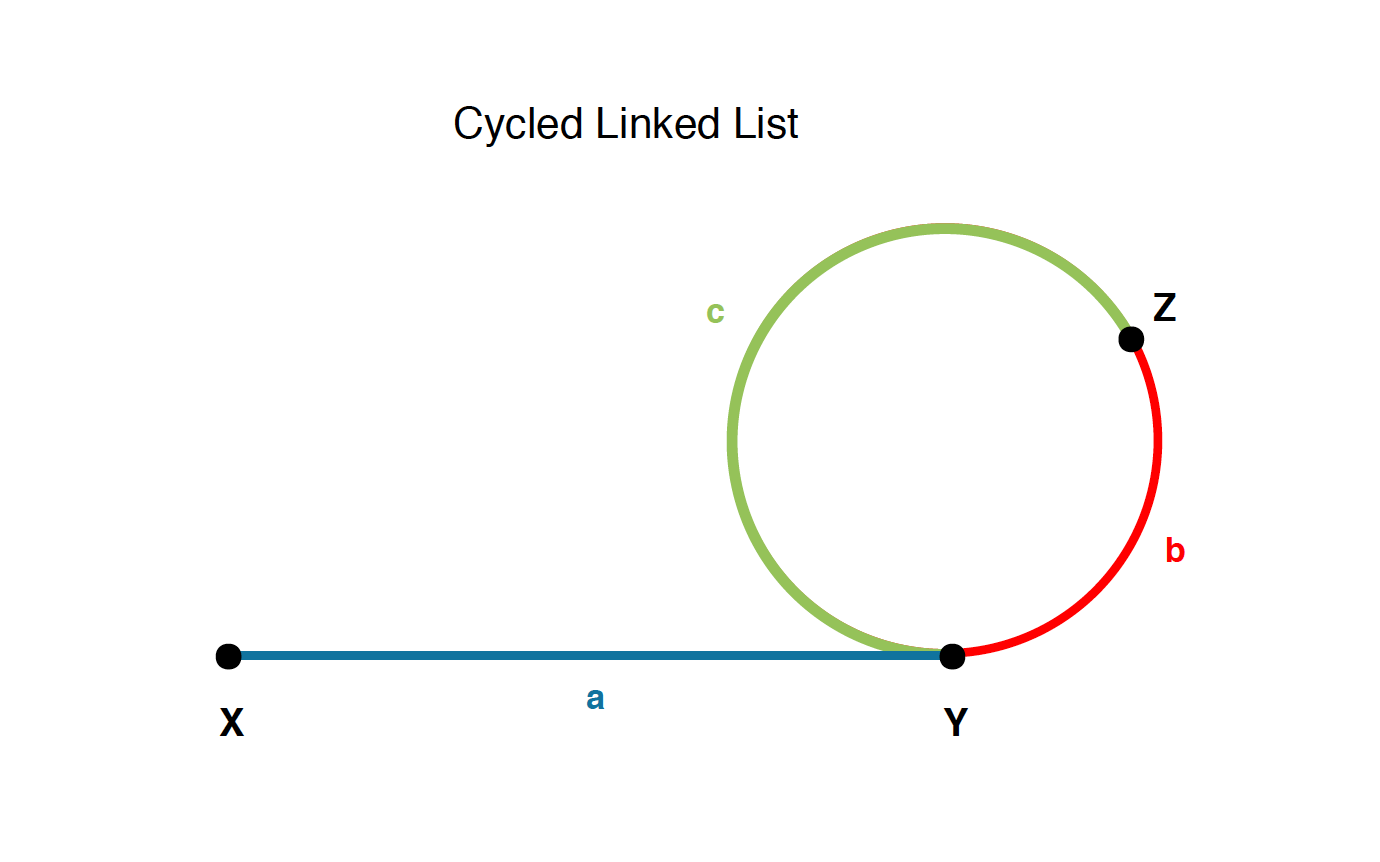
- X is the start node of the linked list.
- Y is the node where the cycle begins. It is the node we are looking for.
- Z is the node where the fast and slow pointers meet for the first time.
- For fast pointer, the distance it has walked through is a + b + c + b; for slow pointer, the distance is a + b. Since the speed of fast pointer is twice of the slow pointer, then we have a + b + c + b = 2 * (a + b). Finally we have
a = c. - When they meet at node Z, we can put fast pointer to the start node X, and let the slow pointer continue walk in the cycle. This time, we let both pointers move one step each time. When they meet again, they should be at node Y, where the cycle begins.
/**
* @param head of the original linked list
* @return middle node of the linked list
*
* Sample
* Input: 7->3->12->8->4->9->12
* Output: 12
* Input: 7->3->12->8->4
* Output: null
*
*/
public ListNode detectCycle(ListNode head) {
if (head == null) {
return null;
}
ListNode fast = head; // ListNode fast = head.next doesn't work
ListNode slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) {
fast = head;
while (fast != slow) {
fast = fast.next;
slow = slow.next;
}
return fast;
}
}
return null;
}
4. Classic Problems
- LeetCode 83 - Remove Duplicates from Sorted List
- LeetCode 82 - Remove Duplicates from Sorted List II
- LeetCode 206 - Reverse Linked List
- LeetCode 92 - Reverse Linked List II
- LeetCode 148 - Sort List
- LeetCode 143 - Reorder List
- LeetCode 141 - Linked List Cycle
- LeetCode 26 - Merge k Sorted Lists
- LeetCode 109 - Convert Sorted List to Binary Search Tree