1113. Data Structure - QueueQueue and FIFO
Implement queue with linked list and array.
1. Queue
1.1 Real-life Example
Queue is similar to the ticket queue outside a cinema hall, where the first person entering the queue is the first person who gets the ticket.
1.2 Queue in Programming Terms
Queue is an abstract data type that serves as a collection of elements, with two principal operations:
enqueue: add an element to the collectiondequeue: remove the least recently added element
Queue follows the FIFO(First-in, first-out) rule. The item that goes in first is the item that comes out first too.
1.3 Common Operations on Queue
- enqueue(item): Add an item to the end of the list.
- dequeue(): Pull the first item out of the list.
- peek(): Return the top of the queue.
- isEmpty(): Return true if and only if the queue is empty.
1.4 Time Complexity
- enqueue: $O(1)$
- dequeue: $O(1)$
- peek: $O(1)$
2. Implementation
Four ways to implement queue.
- Linked List
- Array
- Circular Array
- Stack
2.1 Using Linked List
Use two pointers(head and tail) to locate the first and last nodes in the list and track the change.
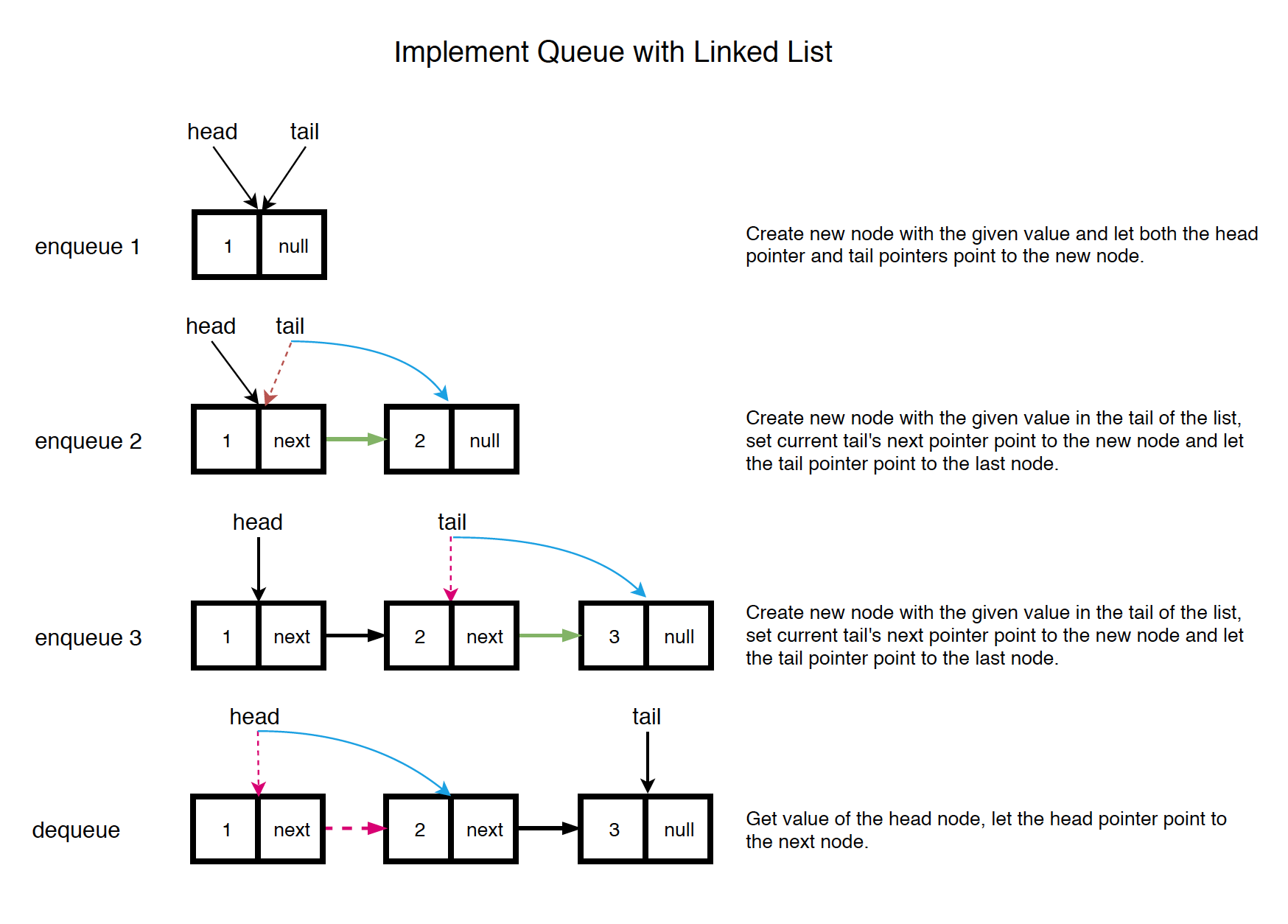
- enqueue: Create new node with the given value in the tail of the list, set current tail’s next pointer point to the new node and let the tail pointer point to the last node.
- dequeue: Get value of the head node, let the head pointer point to the next node.
See the implementation below.
public class LinkedListQueue {
private ListNode head; // the first node
private ListNode tail; // the last node
public LinkedListQueue() {
head = null;
tail = null;
}
// Add item to the tail of the list
public void enqueue(int value) {
if (tail == null) {
tail = new ListNode(value);
head = tail;
} else {
tail.next = new ListNode(value);
tail = tail.next;
}
}
// Remove the head from the list and return its value
public int dequeue() throws Exception {
if (head == null) {
throw new Exception();
}
int value = head.val;
head = head.next;
if (head == null) {
tail = null;
}
return value;
}
// Get the value of the head
public int peek() throws Exception {
if (head == null) {
throw new Exception();
}
return head.val;
}
// Return whether the queue is empty
public boolean isEmpty() {
return head == null;
}
}
2.2 Using Array
Use two pointers(head and tail) to locate the first and last position in the array and track the change.
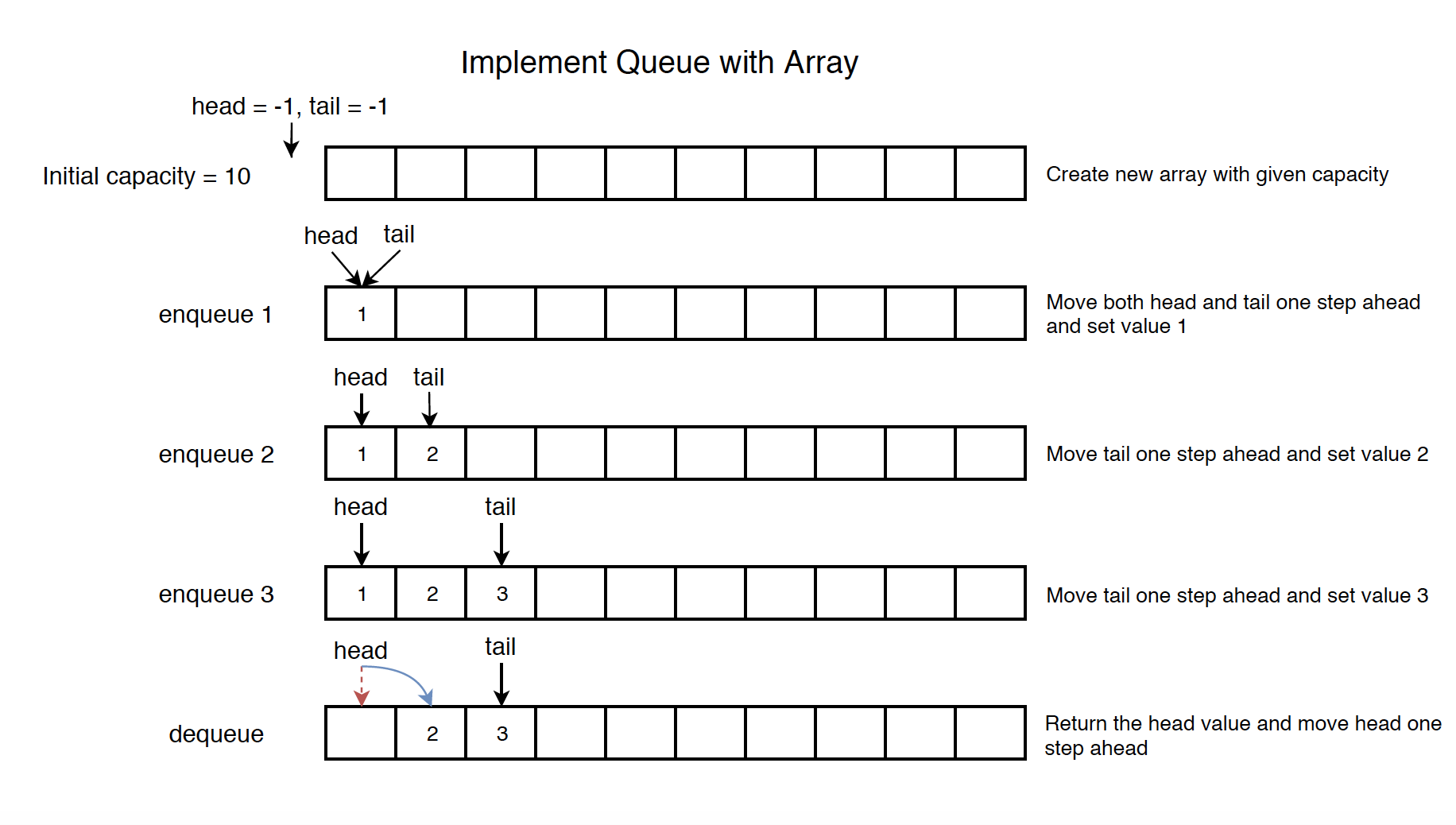
- enqueue: Move tail one step ahead and set value.
- dequeue: Return the head value and move head one step ahead.
See the implementation below.
public class ArrayQueue {
private int head; // the first node
private int tail; // the last node
private int[] arr;
public ArrayQueue(int capacity) {
arr = new int[capacity];
head = -1;
tail = -1;
}
// Add item to the end of the array
public void enqueue(int value) {
if (tail >= arr.length - 1) {
return;
}
arr[++tail] = value;
if (head == -1) {
head = 0;
}
}
// Remove the first item from the array and return its value
public int dequeue() throws Exception {
if (isEmpty()) {
throw new Exception();
}
int value = arr[head];
head++;
return value;
}
// Get the first item
public int peek() throws Exception {
if (isEmpty()) {
throw new Exception();
}
return arr[head];
}
// Return whether the queue is empty
public boolean isEmpty() {
return (head == -1) || (head > tail);
}
}
- There is one problem with the above implementation. Notice that both head and tail only increase, never decrease. When tail reaches to the end of the array, you cannot add more items into it. Even if you call dequeue method to clear some space, however, the head and tail won’t move back.
2.3 Using Circular Array
To solve the issue mentioned above, we can use a circular array to implement the queue.
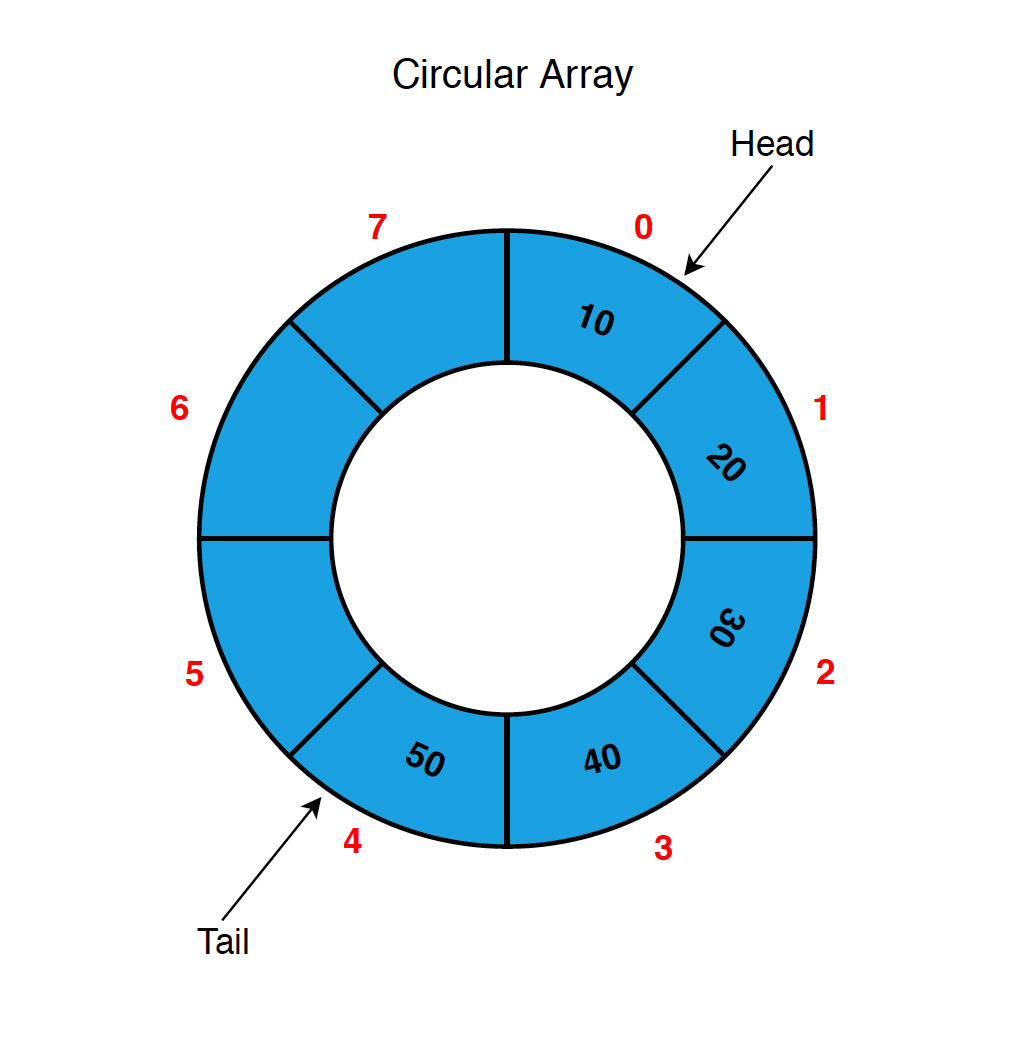See the details below.
Notice the step of ‘enqueue 9’ and ‘dequeue 8’.
- If
tailis at the last position of the array, it will be moved back to the first position if new item needs to be added. - If
headis at the last position of the array, it will be moved back to the first position if old item needs to be deleted.
See the implementation below.
public class CircularArrayQueue {
private int head; // the first node in queue, not the first item in array
private int tail; // the last node in queue, not the first item in array
private int[] arr;
private int size;
public CircularArrayQueue(int capacity) {
arr = new int[capacity];
head = 0;
tail = 0;
size = 0;
}
// Add item to the end of the queue
public void enqueue(int value) {
// check if deque is full
if (isFull()) {
System.out.println("queue is full.");
return;
}
tail = (head + size) % arr.length;
arr[tail] = value;
size += 1;
}
// Remove the first item from the queue and return its value
public int dequeue() throws Exception {
if (isEmpty()) {
throw new Exception("Array Queue is empty when dequeue!");
}
int value = arr[head];
head = (head + 1) % arr.length;
size -= 1;
return value;
}
// Get the first item
public int peek() throws Exception {
if (isEmpty()) {
throw new Exception("Array Queue is empty when peek!");
}
return arr[head];
}
// Return whether the queue is full
public boolean isFull() {
return size == arr.length;
}
// Return whether the queue is empty
public boolean isEmpty() {
return size == 0;
}
}
2.4 Using Stack
Use two stacks. The first one only stores new items, and the second one only stores old items.
import java.util.Stack;
public class StackQueue {
private Stack<Integer> stack1; // s1 stores new items
private Stack<Integer> stack2; // s2 stores old items
public StackQueue() {
stack1 = new Stack<>();
stack2 = new Stack<>();
}
// Add new item onto queue
public void enqueue(int value) {
stack1.push(value);
}
// Remove the first item from the queue and return its value
public int dequeue() throws Exception {
peek();
return stack2.pop();
}
// Get the first element
public int peek() throws Exception {
if (stack2.isEmpty()) {
while (!stack1.isEmpty()) {
stack2.push(stack1.pop());
}
}
if (stack2.isEmpty()) {
throw new Exception();
}
return stack2.peek();
}
// Return whether the queue is empty
public boolean isEmpty() {
return stack1.isEmpty() && stack2.empty();
}
}
- The average time complexity is $O(1)$.
3. Implementing Sorting Algorithms with Queue
3.1 Merge Sort with Queue
If we call the sort method with array {2,4,5,7,1,2,3,6}, it will return a queue, which contains {1,2,2,3,4,5,6,7}, 1 is the header and 7 is the tail.
import java.util.LinkedList;
import java.util.Queue;
public class QueueMergeSort {
// Merge Sort
public Queue<Integer> sort(int[] nums) {
if (nums == null || nums.length == 0) {
return null;
}
// initialize queue
Queue<int[]> queue = new LinkedList<int[]>();
for (int i = 0; i < nums.length; i++) {
// convert number to number array
queue.offer(new int[]{nums[i]});
}
while (queue.size() > 1) {
int[] l = queue.poll();
int[] r = queue.poll();
int[] merged = merge(l, r);
queue.offer(merged);
}
int[] sorted = queue.poll();
Queue<Integer> finalQueue = new LinkedList<>();
for (int i : sorted) {
finalQueue.offer(i);
}
return finalQueue;
}
private int[] merge(int[] nums1, int[] nums2) {
if (nums1 == null || nums1.length == 0) {
return nums2;
}
if (nums2 == null || nums2.length == 0) {
return nums1;
}
int[] nums = new int[nums1.length + nums2.length];
int i = 0, j = 0;
for (int k = 0; k < nums.length; k++) {
if (i >= nums1.length) {
nums[k] = nums2[j];
j++;
} else if (j >= nums2.length) {
nums[k] = nums1[i];
i++;
} else if (nums1[i] <= nums2[j]) {
nums[k] = nums1[i];
i++;
} else {
nums[k] = nums2[j];
j++;
}
}
return nums;
}
}