1128. Data Structure - Fenwick TreeFenwick and Binary Indexed Tree
Use fenwick tree to efficiently solve the prefix sum problem.
1. What is Fenwick Tree?
Binary Indexed Tree also called Fenwick Tree provides a way to represent an array of numbers in an array, allowing prefix sums to be calculated efficiently. For example, an array [2, 3, -1, 0, 6] is given, then the prefix sum of first 3 elements [2, 3, -1] is 2 + 3 + -1 = 4.
Given an array A, and two types of operations are to be performed on it.
- Change the value stored at an index i. (This is called a point update operation)
- Find the sum of a prefix of length k. (This is called a range sum query)
2. Available Solutions
2.1 Naive Solution
A straightforward implementation looks like this.
public class PrefixSumNaive {
private int[] nums;
public PrefixSumNaive(int[] nums) {
this.nums = nums;
}
// update value for the specified index
public void update(int i, int v) {
nums[i] = v;
}
// calculate the sum of all nums[i] such that 0 <= i < k
public int prefixSum(int k) {
int sum = 0;
for (int i = 0; i <= k; i++) {
sum += nums[i];
}
return sum;
}
// calculate the sum of all nums[i] such that start <= i <= end
public int rangeSum(int start, int end) {
int sum = 0;
for (int i = start; i <= end; i++) {
sum += nums[i];
}
return sum;
}
}
- Space Complexity: $O(n)$
- Time Complexity:
- constructor - $O(1)$
- update - $O(1)$
- prefixSum - $O(k)$, worst: $O(n)$,
- rangeSum - $O(end - start)$, worst: $O(n)$
2.2 Improved Solution
Instead of calculate the sum every time for the query, we can store all sum values in a separate array.
public class PrefixSumImproved {
private int[] nums;
private int[] sum;
public PrefixSumImproved(int[] nums) {
this.nums = nums;
this.sum = new int[nums.length];
this.sum[0] = nums[0];
for (int i = 1; i < nums.length; i++) {
this.sum[i] = this.sum[i - 1] + nums[i];
}
}
// update value for the specified index
public void update(int index, int v) {
for (int i = index; i < sum.length; i++) {
sum[i] += v - nums[index];
}
}
// calculate the sum of all nums[i] such that 0 <= i < k
public int prefixSum(int k) {
return sum[k];
}
// calculate the sum of all nums[i] such that start <= i <= end
public int rangeSum(int start, int end) {
if (start == 0) {
return sum[end];
}
return sum[end] - sum[start - 1];
}
}
- Space Complexity: $O(2n)$
- Time Complexity:
- constructor - $O(n)$
- update - $O(n)$
- prefixSum - $O(1)$
- rangeSum - $O(1)$
2.3 Segment Tree
public class SegmentTree {
private SegmentTreeNode root;
public SegmentTree(int[] arr) {
this.root = build(arr, 0, arr.length - 1);
}
private SegmentTreeNode build(int[] arr, int start, int end) {
if (start > end) {
return null;
}
SegmentTreeNode root = new SegmentTreeNode(start, end);
if (start == end) {
root.sum = arr[start];
return root;
}
int mid = start + (end - start) / 2;
root.left = build(arr, start, mid);
root.right = build(arr, mid + 1, end);
root.sum = root.left.sum + root.right.sum;
return root;
}
public int prefixSum(int index) {
return querySum(this.root, 0, index);
}
public int rangeSum(int start, int end) {
return querySum(this.root, start, end);
}
public int querySum(SegmentTreeNode root, int start, int end) {
if (root == null) {
return 0;
}
// case 1: search range is same with the range of root node
if (root.start == start && root.end == end) {
return root.sum;
}
int mid = root.start + (root.end - root.start) / 2;
if (end <= mid) {
// case 2: search range is in the range of left child node
return querySum(root.left, start, end);
} else if (start > mid) {
// case 3: search range is in the range of right child node
return querySum(root.right, start, end);
} else {
//case 4: search range crosses both left and right children
int leftsum = querySum(root.left, start, mid);
int rightsum = querySum(root.right, mid + 1, end);
return leftsum + rightsum;
}
}
public void update(int index, int value) {
update(this.root, index, value);
}
private void update(SegmentTreeNode root, int index, int value) {
if (root == null) {
return;
}
if (root.start == root.end && root.start == index) {
root.sum = value;
return;
}
int mid = root.start + (root.end - root.start) / 2;
if (index <= mid) {
update(root.left, index, value);
} else {
update(root.right, index, value);
}
root.sum = root.left.sum + root.right.sum;
}
class SegmentTreeNode {
public int start, end;
public int sum;
public SegmentTreeNode left, right;
public SegmentTreeNode(int start, int end) {
this.start = start;
this.end = end;
this.left = null;
this.right = null;
}
}
}
- Space Complexity: $O(n)$
- Time Complexity:
- constructor - $O(n)$
- update - $O(\log{}n)$
- prefixSum - $O(\log{}n)$
- rangeSum - $O(\log{}n)$
3. Fenwick Tree Solution
3.1 Basic Idea of Binary Indexed Tree
We know the fact that each integer can be represented as the sum of powers of two. For example, 19 can be represented as 16 + 2 + 1, that is $2^4$ + $2^1$ + $2^0$. 10 can be represented as 8 + 2, that is $2^3$ + $2^1$. We will see how to use this rule in Binary Indexed Tree.
In addition, x & (-x) gives the last set bit in a number.
- If x = 10, its binary representation is 1010. x&(-x) = 1010 & 0110 = 10 = 2(decimal)
- If x = 3, its binary representation is 11. x&(-x) = 011 & 101 = 1(decimal)
3.2 Representation of BIT
Binary Indexed Tree(BIT) is represented as an array. Let the array be BIT[]. Each node of the Binary Indexed Tree stores the sum of some elements of the input array. The size of the Binary Indexed Tree is equal to the size of the input array, denoted as n. In the code below, we use a size of n+1 for ease of implementation.
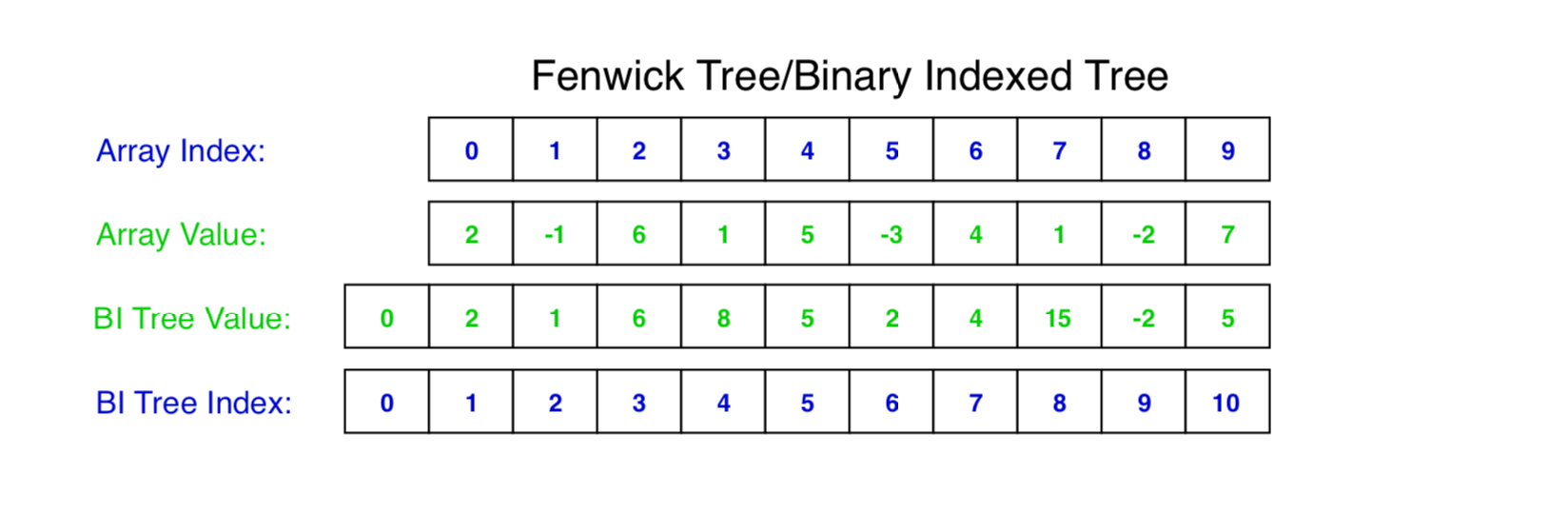
3.3 Get Sum Function
Fenwick Tree is constructed as follows.
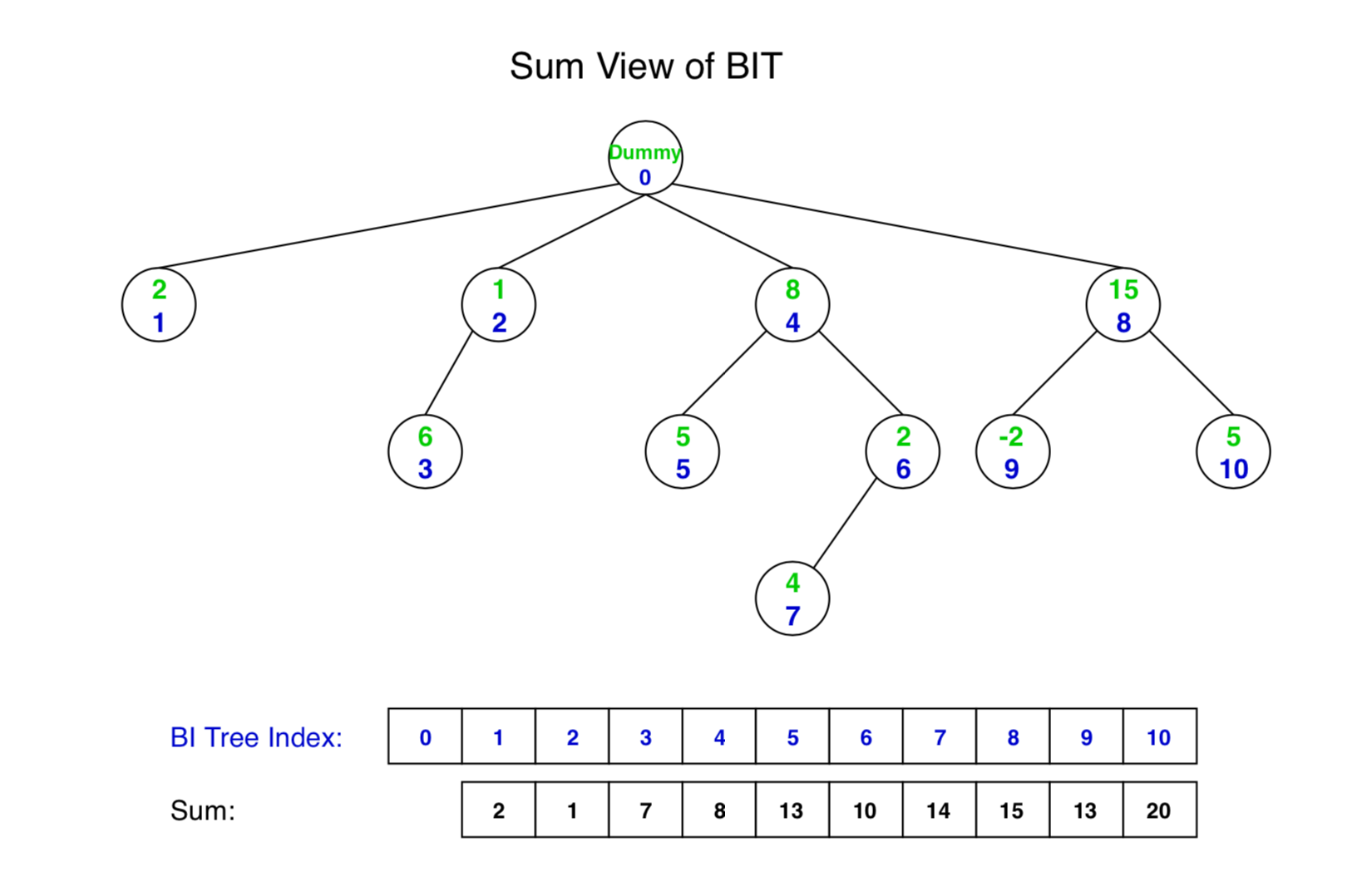 Create method prefixSum() to get the sum for the given index. We just need to summarize all the values along the path from dummy node to targeted node. Here are some examples.
Create method prefixSum() to get the sum for the given index. We just need to summarize all the values along the path from dummy node to targeted node. Here are some examples.
- prefixSum(1) = BIT[1] = 2.
- prefixSum(3) = BIT[3] + BIT[2] = 6 + 1 = 7.
- prefixSum(7) = BIT[7] + BIT[6] + BIT[4]= 4 + 2 + 8 = 14.
- prefixSum(8) = BIT[8] = 15.
- prefixSum(10) = BIT[10] + BIT[8] = 15 + 5 = 20.
To locate the parent node, we can use following formula.
index -= index & (-index);
Below is another view of the BIT, which helps to understand how getsum works.
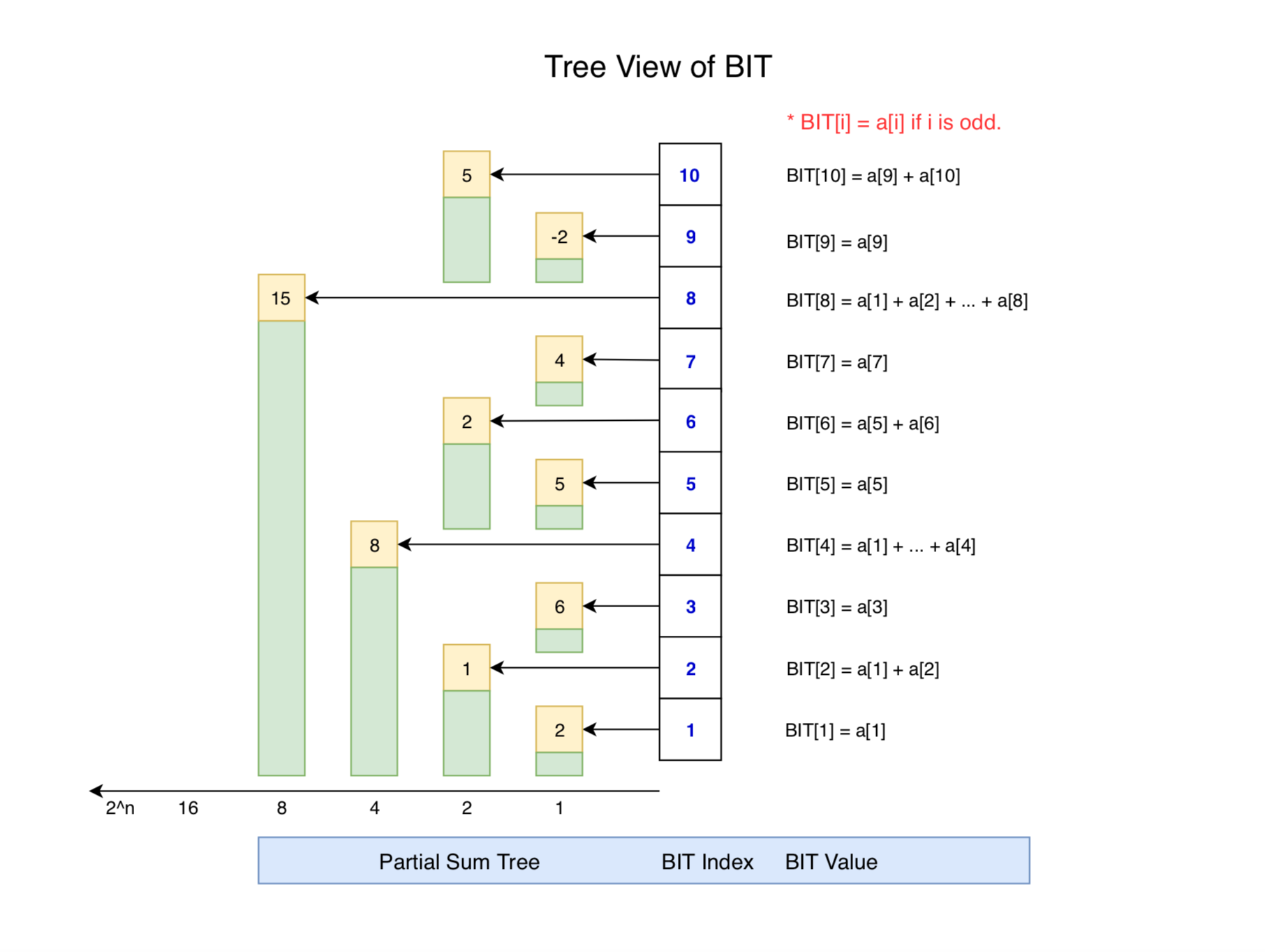
- prefixSum(10) = range(1, 8) + range(9, 10) = BIT[8] + BIT[10]
- prefixSum(8) = range(1, 8) = BIT[8]
- prefixSum(7) = range(1, 4) + range(5, 6) + range(7) = BIT[4] + BIT[6] + BIT[7]
- prefixSum(2) = range(1, 2) = BIT[2]
- prefixSum(1) = range(1, 1) = BIT[1]
3.4 Update Function
The update function needs to make sure that all the BIT nodes which contain arr[i] within their ranges being updated. We loop over such nodes in the BIT by repeatedly adding the decimal number corresponding to the last set bit of the current index. Notice that the import parameter is the ‘delta value’ not an absolute value. For example, if the original array is [2, -1, 6, 1, 5, -3, 4, 1, -2, 7] and we want to update the second element arr[1] to 2, we should put 3 as import parameter when calling update() method.
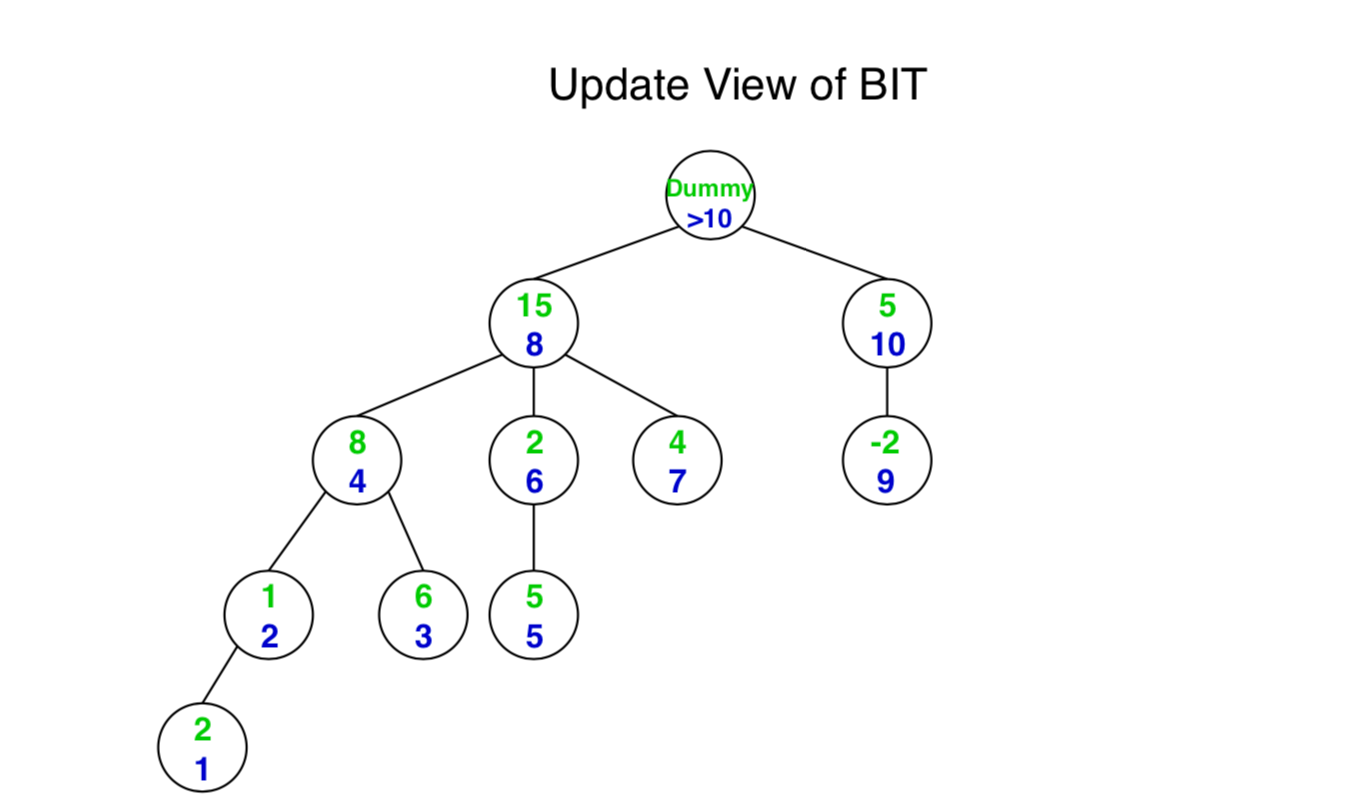 Here are some examples.
Here are some examples.
- To update node1(BIT[1]), we need to update BIT[1], BIT[2], BIT[4], BIT[8].
- To update node2(BIT[2]), we need to update BIT[2], BIT[4], BIT[8].
- To update node8(BIT[8]), we need to update BIT[8] only.
- To update node10(BIT[10]), we need to update BIT[8] only.
- To update nod9(BIT[9]), we need to update BIT[9], BIT[10].
To locate the parent node, we can use following formula.
index += index & (-index);
3.5 Implementation
Create class named FenwickTree with two important methods.
- prefixSum(index) - get the pre sum from 0…index.
- update(index, value) - update with the given index and value(delta).
public class FenwickTree {
int[] BIT;
public FenwickTree(int arr[]) {
BIT = new int[arr.length + 1]; // index starts from 1 not 0.
// store the actual values in BIT[] using update()
for (int i = 0; i < arr.length; i++) {
update(i, arr[i]);
}
}
// return sum of arr[0..index].
public int prefixSum(int index) {
int sum = 0;
// index in BIT[] starts from 1
index = index + 1;
// traverse ancestors of BIT[index]
while (index > 0) {
// add current element of BIT to sum
sum += BIT[index];
// move index to parent node in Sum View
index -= index & (-index);
}
return sum;
}
// return sum of the given range
public int rangeSum(int from, int to) {
if (from >= 0 && to >= 0 && to >= from) {
return prefixSum(to) - prefixSum(from - 1);
} else {
return -1;
}
}
// update a node in Binary Index Tree at given index, the given value is the 'delta' value
// compared with the original array arr[], not array BIT[]. This delta value is added to BIT[i] and
// all of its ancestors.
public void update(int index, int val) {
// index in BIT[] starts from 1
index = index + 1;
// traverse all ancestors and add 'val'
while (index <= BIT.length) {
// add 'val' to current node of BI Tree
BIT[index] += val;
// update index to that of parent in Update View
index += index & (-index);
}
}
}
- Space Complexity: $O(n)$
- Time Complexity:
- constructor - $O(n)$
- update - $O(\log{}n)$
- prefixSum - $O(\log{}n)$
- rangeSum - $O(\log{}n)$
Simplified version of BIT.
public class FenwickTreeSimplified {
int[] BIT;
public FenwickTreeSimplified(int arr[]) {
BIT = new int[arr.length + 1];
for (int i = 0; i < arr.length; i++) {
update(i, arr[i]);
}
}
public int prefixSum(int index) {
int sum = 0;
index++;
for(; index > 0; index -= index&-index)
sum += BIT[index];
return sum;
}
public int rangeSum(int from, int to) {
if (from >= 0 && to >= 0 && to >= from) {
return prefixSum(to) - prefixSum(from - 1);
} else {
return -1;
}
}
public void update(int index, int val) {
index++;
for(; index <= BIT.length; index += index&-index)
BIT[index] += val;
}
}
4. Performance Comparison
| Solution | Space Complexity | Construct | Update | Get Sum | Range Sum |
|---|---|---|---|---|---|
| Naive | $O(n)$ | $O(1)$ | $O(1)$ | $O(n)$ | $O(n)$ |
| Improved | $O(2n)$ | $O(n)$ | $O(n)$ | $O(1)$ | $O(1)$ |
| Segment Tree | $O(n)$ | $O(n)$ | $O(\log{}n)$ | $O(\log{}n)$ | $O(\log{}n)$ |
| Fenwick Tree | $O(n)$ | $O(n)$ | $O(\log{}n)$ | $O(\log{}n)$ | $O(\log{}n)$ |
- Fenwick Tree has same performance with segment tree, but it is much easier to implement BIT than segment tree.
- If update operation is rare, we should use the improved solution.
- If update operation is frequent, then we should use either segment tree or fenwick tree.