1224. Algorithm - Matrix DP
DP

Introduce dynamic programming.

Minimum Path Sum

  • Follow up: print the path?

2. Matrix DP

2.1 Unique Paths

2.1.1 Problem Description

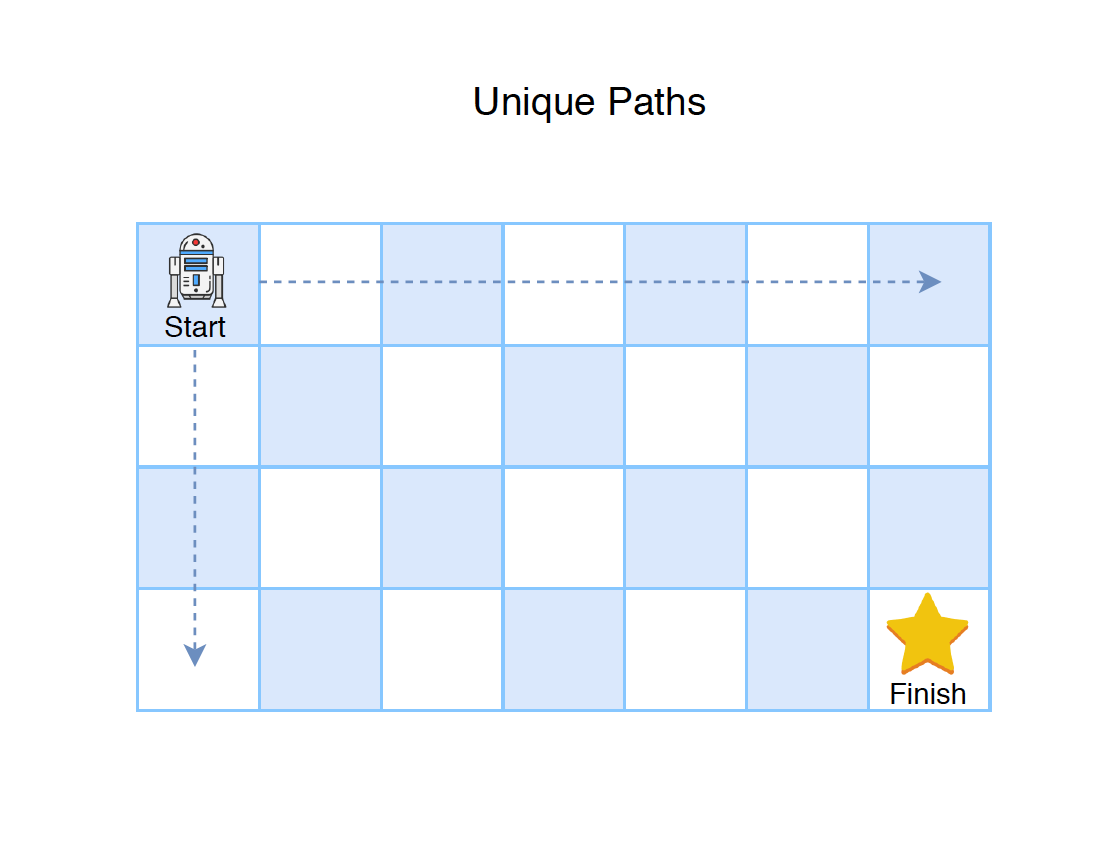
A robot is located at the top-left corner of a m x n grid (marked ‘Start’ in the diagram below). The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below). How many possible unique paths are there? image

2.1.2 Solution with Matrix(Two-dimensional array)

// time: O(m*n), space: O(m*n)
public int uniquePathMatrix(int m, int n) {
    if (m <= 0 || n <= 0) {
        return 0;
    }

    int[][] dp = new int[m][n];
    // Initialization
    for (int i = 0; i < m; i++) {
        dp[i][0] = 1;
    }
    for (int j = 0; j < n; j++) {
        dp[0][j] = 1;
    }
    // Calculate dp[i][j]
    for (int i = 1; i < m; i++) {
        for (int j = 1; j < n; j++) {
            dp[i][j] = dp[i][j - 1] + dp[i - 1][j];
        }
    }

    return dp[m - 1][n - 1];
}

// time: O(m*n), space: O(m*n), without separated initialization
public int uniquePathMatrix2(int m, int n) {
    if (m <= 0 || n <= 0) {
        return 0;
    }

    int[][] dp = new int[m][n];
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (i == 0 || j == 0) {
                dp[i][j] = 1;
            } else {
                dp[i][j] = dp[i][j - 1] + dp[i - 1][j];
            }
        }
    }

    return dp[m - 1][n - 1];
}
  • Time complexity: $O(m*n)$
  • Space complexity: $O(m*n)$

2.1.3 Solution with One-dimensional Array

Use one-dimensional array instead of the matrix. Same time complexity, but space is reduced to $O(n)$.

// time: O(m*n), space: O(n)
public int uniquePathArray(int m, int n) {
    if (m <= 0 || n <= 0) {
        return 0;
    }

    int[] dp = new int[n];
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (j == 0) {
                dp[j] = 1;
            } else {
                dp[j] = dp[j] + dp[j - 1];
            }
        }
    }

    return dp[n - 1];
}

// time: O(m*n), space: O(n), without checking the first column
public int uniquePath(int m, int n) {
    if (m <= 0 || n <= 0) {
        return 0;
    }

    int[] dp = new int[n];
    dp[0] = 1;
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (j > 0) {
                dp[j] = dp[j] + dp[j - 1];
            }
        }
    }

    return dp[n - 1];
}
  • Time complexity: $O(m*n)$
  • Space complexity: $O(n)$

2.2 Define Matrix with Larger Size

When to define a dp matrix with m+1 and n+1? see question LeetCode 221 - Maximal Square.

2.3 Classic Problems

6. Source Files

7. References