1213. Algorithm - Divide and Conquer
Divide and Conquer

Divide and Conquer.

1. Divide and Conquer

1.1 Basic Concepts

Divide and Conquer is an algorithmic paradigm. A typical Divide and Conquer algorithm solves a problem using following three steps.

  • Divide: Break the given problem into subproblems of same type.
  • Conquer: Recursively solve these subproblems
  • Combine: Appropriately combine the answers

1.2 Typical Algorithms:

  • Merge Sort
  • Binary Search

1.3 Merge Sort

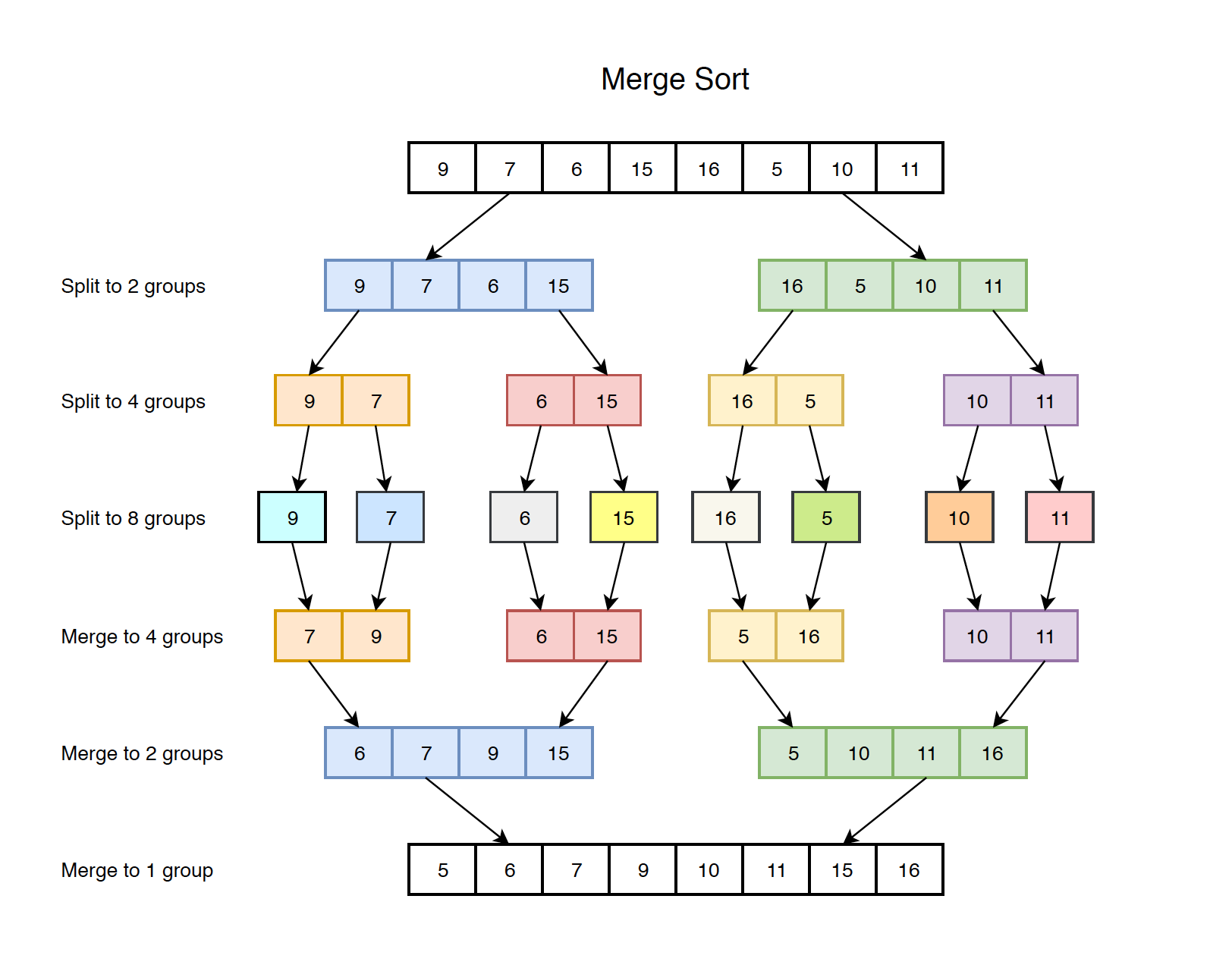
A classic example of Divide and Conquer is Merge Sort demonstrated below. In Merge Sort, we divide array into two halves, sort the two halves recursively, and then merge the sorted halves. image

Implementation:

public void mergeSort(int[] nums) {
    if (nums == null || nums.length < 2) {
        return;
    }
    mergeHelper(nums, 0, nums.length - 1);
    return;
}

private void mergeHelper(int[] nums, int start, int end) {
    if (start >= end) {
        return;
    }

    int mid = start + (end - start) / 2;
    mergeHelper(nums, start, mid);
    mergeHelper(nums, mid + 1, end);
    merge(nums, start, mid, end);
}

private void merge(int[] nums, int start, int mid, int end) {
    int[] copy = Arrays.copyOf(nums, nums.length);

    int left = start;
    int right = mid + 1;
    for (int k = start; k <= end; k++) {
        if (left > mid) { // no item at left
            nums[k] = copy[right];
            right++;
        }
        else if(right > end) { // no item at right
            nums[k] = copy[left];
            left++;
        }
        else if (copy[left] <= copy[right]) {
            nums[k] = copy[left];
            left++;
        }
        else{
            nums[k] = copy[right];
            right++;
        }
    }
}

Binary Search is a searching algorithm. In each step, the algorithm compares the input element x with the value of the middle element in array. If the values match, return the index of middle. Otherwise, if x is less than the middle element, then the algorithm recurs for left side of middle element, else recurs for right side of middle element.

Implementation:

public int search(int[] nums, int target) {
    if (nums == null || nums.length == 0) {
        return -1;
    }

    int start = 0;
    int end = nums.length - 1;
    while (start + 1 < end) {
        int mid = start + (end - start) / 2;
        if (nums[mid] == target) {
            return mid;
        } else if (nums[mid] < target) {
            start = mid + 1;
        } else {
            end = mid - 1;
        }
    }

    if (nums[start] == target) {
        return start;
    }
    if (nums[end] == target) {
        return end;
    }
    return -1;
}

2. Sort Linked List

2.1 Description

Sort a linked list in O(nlog(n)) time using constant space complexity.

Example 1:

Input: 4->2->1->3
Output: 1->2->3->4

Example 2:

Input: -1->5->3->4->0
Output: -1->0->3->4->5

2.2 Solution

Find the middle element, partition the list into two sub lists. Sort them separately, then merge the results.

public ListNode sortList(ListNode head) {
    if (head == null || head.next == null) {
        return head;
    }

    ListNode fast = head.next;
    ListNode slow = head;
    while (fast != null && fast.next != null) {
        fast = fast.next.next;
        slow = slow.next;
    }

    ListNode right = sortList(slow.next);
    slow.next = null;
    ListNode left = sortList(head);
    return merge(left, right);
}

public ListNode merge(ListNode l1, ListNode l2) {
    if (l1 == null) {
        return l2;
    }
    if (l2 == null) {
        return l1;
    }

    ListNode dummy = new ListNode(0);
    ListNode curr = dummy;
    while (l1 != null && l2 != null) {
        if (l1.val <= l2.val) {
            curr.next = l1;
            l1 = l1.next;
        } else {
            curr.next = l2;
            l2 = l2.next;
        }
        curr = curr.next;
    }

    if (l1 != null) {
        curr.next = l1;
    }
    if (l2 != null) {
        curr.next = l2;
    }

    return dummy.next;
}

3. Using Divide & Conquer for Tree Problems

3.1 Binary Tree Traversal

Given a binary tree, return the preorder/inorder/postorder traversal of its nodes’ values.

Input: [1,null,2,3]
   1
    \
     2
    /
   3

Preorder: [1,2,3]

// Divide and conquer (recursion)
public List<Integer> preorderTraversal(TreeNode root) {
    List<Integer> ans = new ArrayList<Integer>();
    if (root == null) {
        return ans;
    }

    List<Integer> left = preorderTraversal(root.left);
    List<Integer> right = preorderTraversal(root.right);

    ans.add(root.val);
    ans.addAll(left);
    ans.addAll(right);
    return ans;
}

Inorder: [1,3,2]

// Divide and conquer (recursion)
public List<Integer> inorderTraversal(TreeNode root) {
    List<Integer> ans = new ArrayList<Integer>();
    if (root == null) {
        return ans;
    }

    List<Integer> left = inorderTraversal(root.left);
    List<Integer> right = inorderTraversal(root.right);

    ans.addAll(left);
    ans.add(root.val);
    ans.addAll(right);
    return ans;
}

Postorder: [3,2,1]

// Divide and conquer (recursion)
public List<Integer> postorderTraversal2(TreeNode root) {
    List<Integer> ans = new ArrayList<Integer>();
    if(root == null) {
        return ans;
    }

    List<Integer> left = postorderTraversal(root.left);
    List<Integer> right = postorderTraversal(root.right);

    ans.addAll(left);
    ans.addAll(right);
    ans.add(root.val);
    return ans;
}

3.2 Merge Two Binary Trees

Given two binary trees and imagine that when you put one of them to cover the other, some nodes of the two trees are overlapped while the others are not. You need to merge them into a new binary tree. The merge rule is that if two nodes overlap, then sum node values up as the new value of the merged node. Otherwise, the NOT null node will be used as the node of new tree.

Example:

Input:
	Tree 1                     Tree 2                  
          1                         2                             
         / \                       / \                            
        3   2                     1   3                        
       /                           \   \                      
      5                             4   7                  
Output:
Merged tree:
	     3
	    / \
	   4   5
	  / \   \
	 5   4   7

Solution:

public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
    if (t1 == null) {
        return t2;
    }

    if (t2 == null) {
        return t1;
    }

    TreeNode root = new TreeNode(t1.val + t2.val);
    root.left = mergeTrees(t1.left, t2.left);
    root.right = mergeTrees(t1.right, t2.right);
    return root;
}

4. Divide and Conquer Problems

5. References