1217. Algorithm - Union FindDisjoint Set, Union, and Find
Use Union-Find approach for solve disjoint set problems.
1. Disjoint Set
1.1 Disjoint Set in Math
In mathematics, two sets are said to be disjoint sets if they have no element in common. Equivalently, disjoint sets are sets whose intersection is the empty set. For example, {1, 2, 3} and {4, 5, 6} are disjoint sets, while {1, 2, 3} and {3, 4, 5} are not.
1.2 Disjoint-set Data Structure
A disjoint-set data structure is a data structure that tracks a set of elements partitioned into a number of disjoint (non-overlapping) subsets. Generally, it is implemented with an array and find, union methods.
1.3 Set Problem
Consider a situation with a number of persons and following tasks to be performed on them.
- Add a new friendship relation, i.e., a person
ibecomes friend of another personj. - Find whether individual
iis a friend of individualj(direct or indirect friend).
2. Union Find
A union-find algorithm is an algorithm that performs two useful operations on such a Disjoint-set data structure:
Find: Determine which subset a particular element is in. This can be used for determining if two elements are in the same subset.Union: Join two subsets into a single subset.
Below is the sample code which implements union-find algorithm.
public class DSU { // Disjoint Set Union
public int[] parents;
public DSU(int size) {
parents = new int[size];
for (int i = 0; i < parents.length; i++) {
// Initially, all elements are in their own set.
parents[i] = i;
}
}
// find
public int find(int i) {
if (parents[i] != i) {
return find(parents[i]);
}
return parents[i];
}
// union
public void union(int i, int j) {
int p1 = find(i);
int p2 = find(j);
parents[p1] = p2;
}
}
- Array
parentsstores the information that who is the parent of the current node.
Let’s take a look how it works.
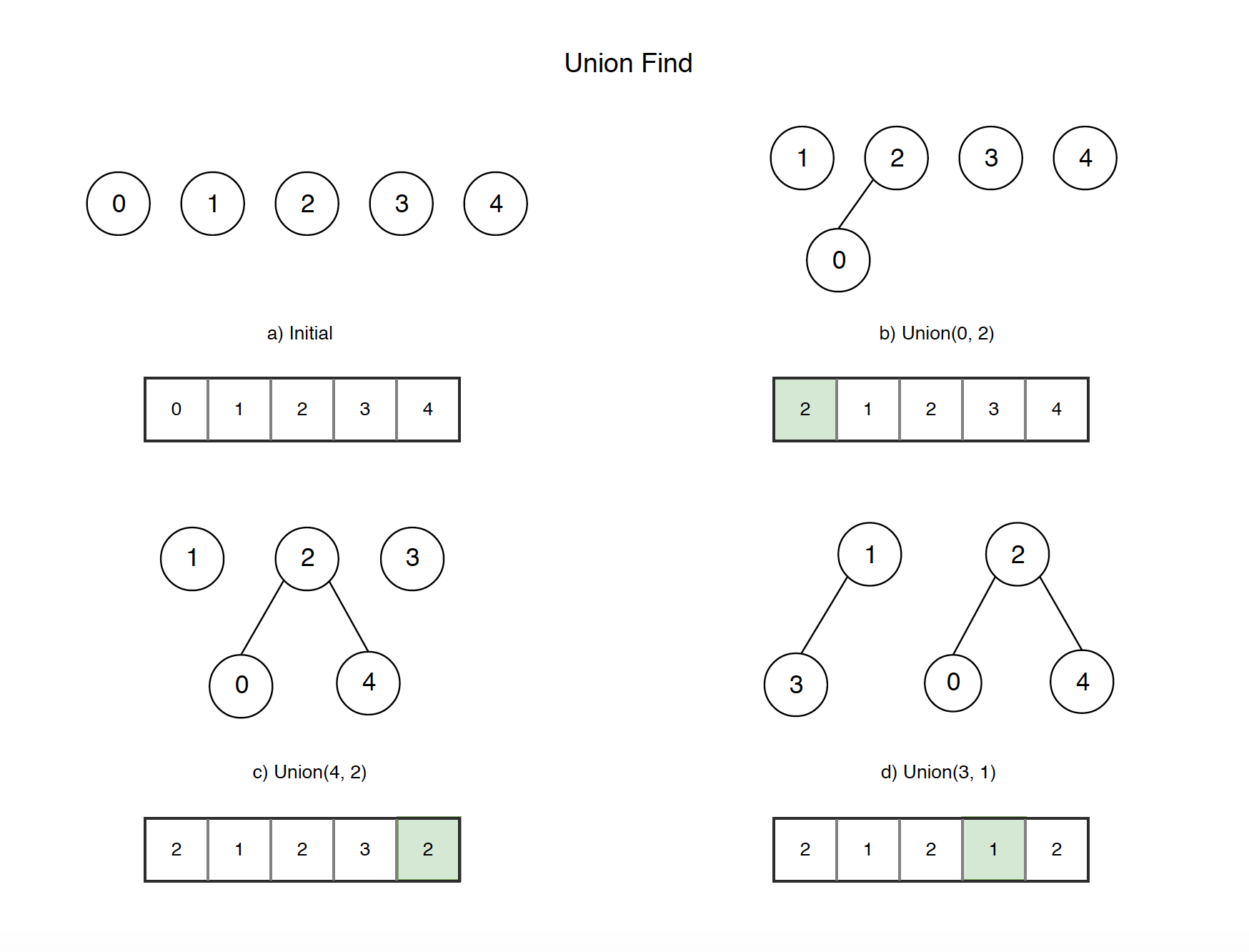
- a) Initially, we have 5 elements and each of them in their own subset.
- b) Call ‘union(0,2)’ to set parent node 2 for node 0. Notice, the value at position 0 of the array is changed to 2.
- c) Call ‘union(4,2)’ to set parent node 2 for node 4. Notice, the value at position 4 of the array is changed to 2.
- d) Call ‘union(3,1)’ to set parent node 1 for node 3. Notice, the value at position 3 of the array is changed to 1.
- Finally, we have two subsets, one is {0,2,4}, another is {1,3}.
Now, if we want to find out whether 0 and 4 are in the same subset, we just need to call find(0) and find(4), then compare the results. If both return the same parent, then they are in the same subset.
The following code show how to use union and find methods to reproduce the above process.
DSU dju = new DSU(5); // parents = [0,1,2,3,4]
// set 2 as parent of 0
dju.union(0, 2); // parents = [2,1,2,3,4]
// set 2 as parent of 4
dju.union(4, 2); // parents = [2,1,2,3,2]
// set 1 as parent of 3
dju.union(3, 1); // parents = [2,1,2,1,2]
// Group1 = {0,2,4}
// Group2 = {1,3}
// Check if 0 and 4 are in the same group.
if(dju.find(0) == dju.find(4)) {
System.out.println("Yes");
}
// Check if 0 and 1 are in the same group.
if(dju.find(0) != dju.find(1)) {
System.out.println("No");
}
3. Optimization
Both the find() and union() methods can be optimized.
- find() - Path Compression
- union() - Union by Rank
3.1 Path Compression
The idea of Path Compression is to flatten the tree when find() is called. The naive find() method is read-only. When find() is called for an element i, root of the tree is returned. The find() operation traverses up from i to find root. The idea of path compression is to make the found root as parent of i so that we don’t have to traverse all intermediate nodes again. If i is root of a subtree, then path (to root) from all nodes under i also compresses.
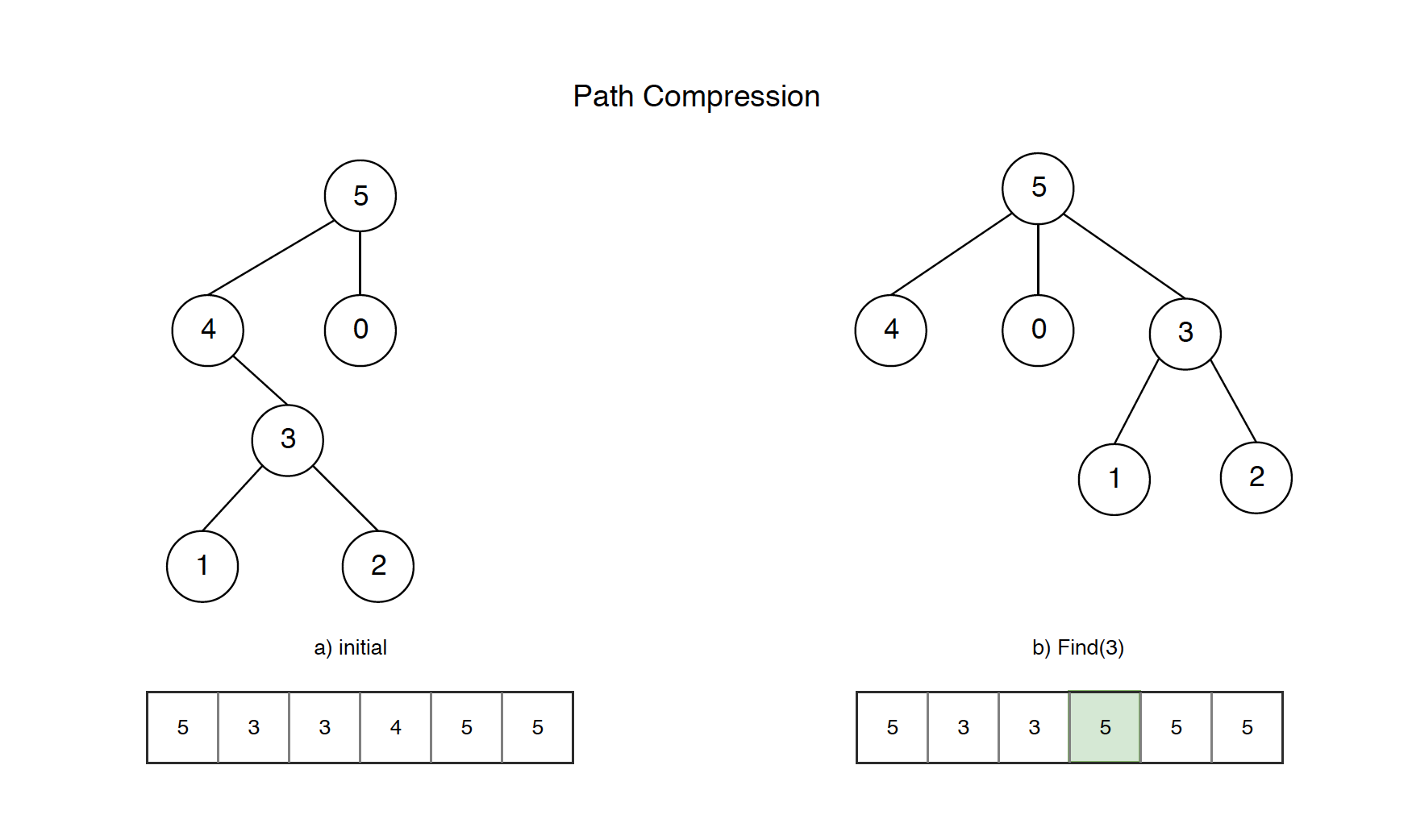
- If we call naive find(3), the tree(array) remains unchanged. The next time you call find(3), it again traverses up from node 4 to node 5.
- With the optimized find() method, the parent of node 3 is updated after calling find(3). When you call find(3) for the second time, it returns parent node 5 directly. Actually, the path for node 3 and its children(node 1 and node 2) are all compressed.
Below is the optimized find() method with Path Compression.
// Path Compression
public int find(int i) {
if (parents[i] != i) {
parents[i] = find(parents[i]);
}
return parents[i];
}
We can also implement find without recursion.
// Path Compression
public int find(int i) {
while (parents[i] != i) {
parents[i] = parents[parents[i]];
i = parents[i];
}
return parents[i];
}
3.2 Union by Rank
Problem with naive union method. Following is an example of worst case scenario. Union the nodes in sequence, the tree becomes like a linked list.
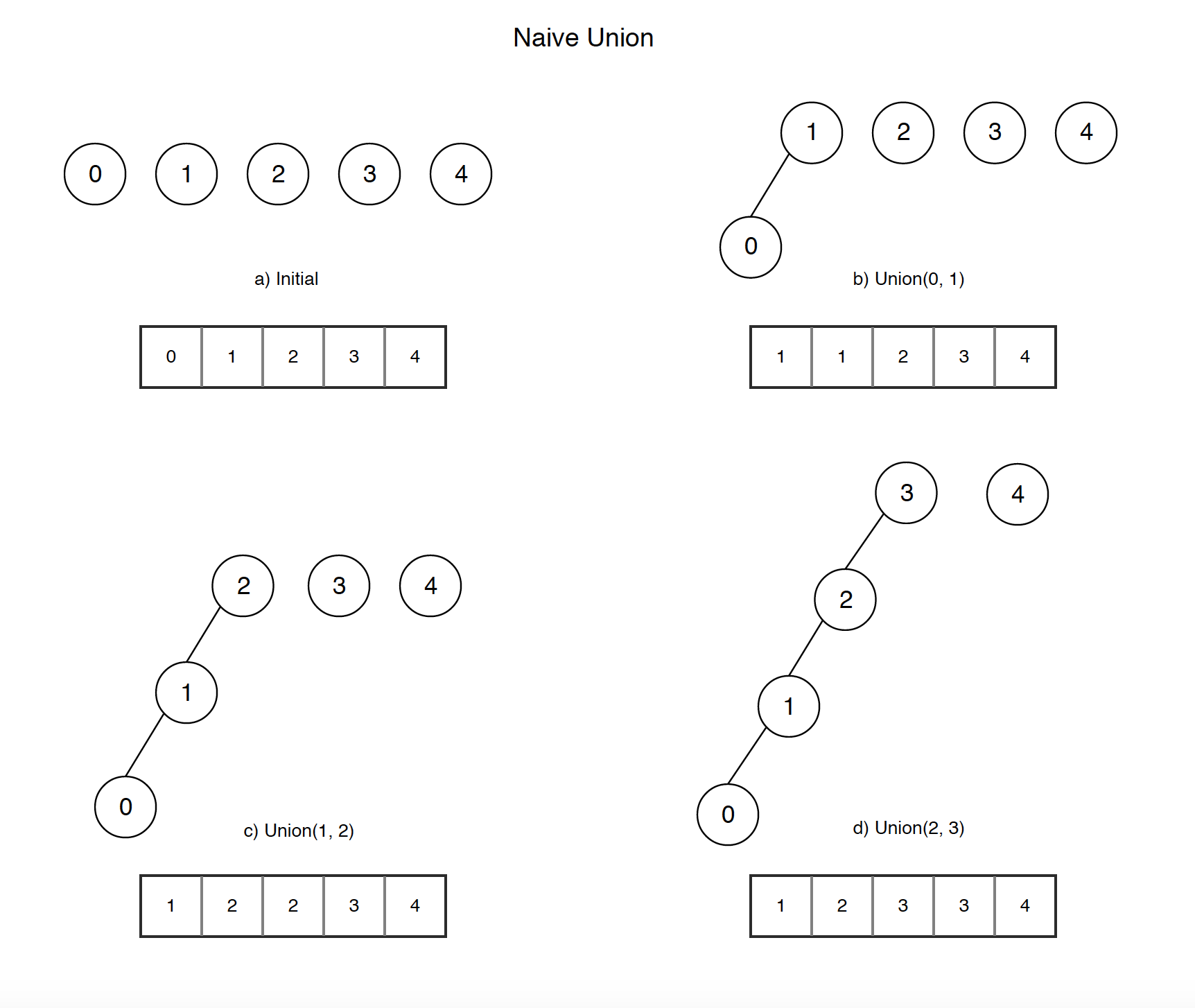
- If we call find(0) after the last step d), it will traverse up from node 0 to node 1, node 2, …, inefficient.
The solution is to always attach smaller depth tree under the root of the deeper tree.
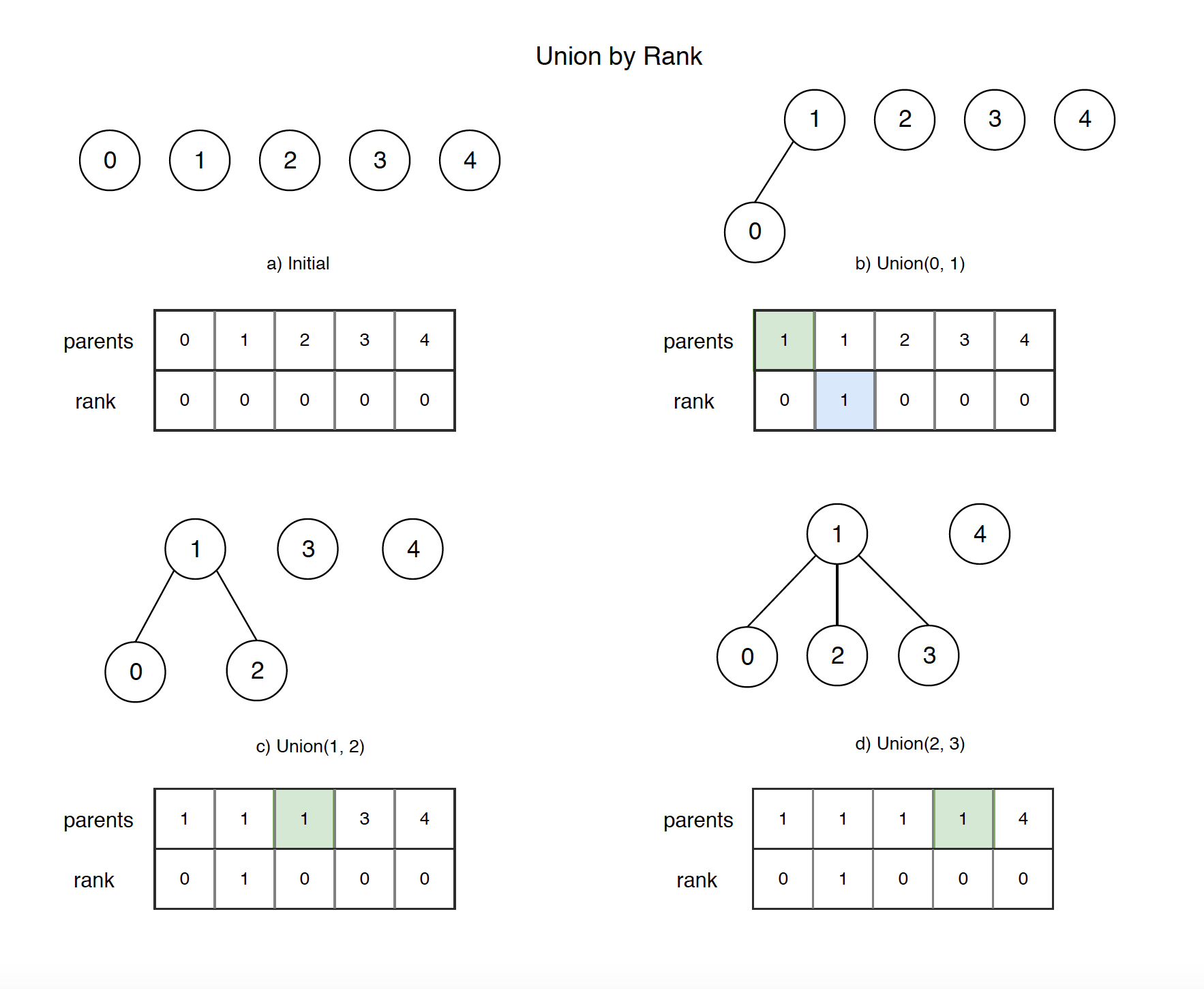
- a) Initially, we have 5 elements and each of them in their own subset. In addition, we have same size rank array, the default value is zero.
- b) When calling ‘union(0,1)’, node 0 and node 1 have the same rank 0. We can choose either of them as the root. In this case, we choose node 1 as root, so set parents[0] = 1. Since node 1 is now as root, so set rank[1] = 1.
- c) When calling ‘union(1,2)’, node 1 has larger rank than node 2, so take node 1 as root, set parents[2] = 1.
- d) When calling ‘union(2,3)’, node 2’s root is node 1 and node 1 has larger rank than node 3, so take node 1 as root, set parents[3] = 1.
- Finally, we have two trees, one is {0,1,2,3}, another is {4}. Notice, tree {0,1,2,3} is flattened.
Below is the optimized union() method with Union by Rank.
// Union by rank
public void union(int i, int j) {
int p1 = find(i);
int p2 = find(j);
if (p1 == p2) {
return;
}
// If root1’s rank is less than root2’s rank
if (rank[p1] < rank[p2]) {
// Then move root1 under root2
parents[p1] = p2;
// If root1’s rank is larger than root2’s rank
} else if (rank[p1] > rank[p2]) {
// Then move root2 under root1
parents[p2] = p1;
// if ranks are the same
} else {
// Then move root1 under root2 (doesn't matter which one goes where)
parents[p1] = p2;
rank[p2]++;
}
}
4. Union Find Template
Based on the above discussion, here is the template for Union and Find.
4.1 Without Path Compression and Rank
public class DSU {
public int[] parents;
public DSU(int size) {
parents = new int[size];
for (int i = 0; i < parents.length; i++) {
// Initially, all elements are in their own set.
parents[i] = i;
}
}
public int find(int i) {
while (parents[i] != i) {
i = parents[i];
}
return parents[i];
}
public void union(int i, int j) {
int p1 = find(i);
int p2 = find(j);
parents[p1] = p2;
}
}
4.2 With Path Compression and Rank
public class DSU { // Disjoint Set Union with Rank
public int[] parents;
public int[] rank;
public DSU(int size) {
parents = new int[size];
for (int i = 0; i < parents.length; i++) {
// Initially, all elements are in their own set.
parents[i] = i;
}
rank = new int[size];
}
// Path Compression
public int find(int i) {
while (parents[i] != i) {
parents[i] = parents[parents[i]];
i = parents[i];
}
return parents[i];
}
// Union by rank
public void union(int i, int j) {
int p1 = find(i);
int p2 = find(j);
if (p1 == p2) {
return;
}
// If root1’s rank is less than root2’s rank
if (rank[p1] < rank[p2]) {
// Then move root1 under root2
parents[p1] = p2;
// If root1’s rank is larger than root2’s rank
} else if (rank[p1] > rank[p2]) {
// Then move root2 under root1
parents[p2] = p1;
// if ranks are the same
} else {
// Then move root1 under root2 (doesn't matter which one goes where)
parents[p1] = p2;
rank[p2]++;
}
}
}
5. Friend Circles
5.1 Description
There are N students in a class. Some of them are friends, while some are not. Their friendship is transitive in nature. For example, if A is a direct friend of B, and B is a direct friend of C, then A is an indirect friend of C. And we defined a friend circle is a group of students who are direct or indirect friends.
Given a N*N matrix M representing the friend relationship between students in the class. If M[i][j] = 1, then the ith and jth students are direct friends with each other, otherwise not. And you have to output the total number of friend circles among all the students.
Example 1:
Input:
[[1,1,0],
[1,1,0],
[0,0,1]]
Output: 2
Explanation:The 0th and 1st students are direct friends, so they are in a friend circle.
The 2nd student himself is in a friend circle. So return 2.
Example 2:
Input:
[[1,1,0],
[1,1,1],
[0,1,1]]
Output: 1
Explanation:The 0th and 1st students are direct friends, the 1st and 2nd students are direct friends,
so the 0th and 2nd students are indirect friends. All of them are in the same friend circle, so return 1.
5.2 Solution with DFS
Search and add friend to group, then count how many groups.
// dfs
public int findCircleNum(int[][] M) {
int[] visited = new int[M.length];
int count = 0;
for (int i = 0; i < M.length; i++) {
if (visited[i] == 0) {
dfs(M, visited, i);
count++;
}
}
return count;
}
public void dfs(int[][] M, int[] visited, int i) {
for (int j = 0; j < M.length; j++) {
if (M[i][j] == 1 && visited[j] == 0) {
visited[j] = 1;
dfs(M, visited, j);
}
}
}
5.3 Solution With Union Find Template
public int findCircleNum(int[][] M) {
DSU dsu = new DSU(M.length);
for (int i = 0; i < M.length - 1; i++) {
for (int j = i + 1; j < M.length; j++) {
if (M[i][j] == 1) {
dsu.union(i, j);
}
}
}
return dsu.count;
}
class DSU { // Disjoint Set Union with Rank
public int[] parents;
public int[] rank;
public int count; // number of groups
public DSU(int size) {
parents = new int[size];
for (int i = 0; i < parents.length; i++) {
// Initially, all elements are in their own set.
parents[i] = i;
}
rank = new int[size];
count = size;
}
// Path Compression
public int find(int i) {
while (parents[i] != i) {
parents[i] = parents[parents[i]];
i = parents[i];
}
return parents[i];
}
// Union by rank
public void union(int i, int j) {
int p1 = find(i);
int p2 = find(j);
if (p1 == p2) {
return;
}
// If root1’s rank is less than root2’s rank
if (rank[p1] < rank[p2]) {
// Then move root1 under root2
parents[p1] = p2;
// If root1’s rank is larger than root2’s rank
} else if (rank[p1] > rank[p2]) {
// Then move root2 under root1
parents[p2] = p1;
// if ranks are the same
} else {
// Then move root1 under root2 (doesn't matter which one goes where)
parents[p1] = p2;
rank[p2]++;
}
count--;
}
}
6. Linked List Components
6.1 Description
We are given head, the head node of a linked list containing unique integer values. We are also given the list G, a subset of the values in the linked list.
Return the number of connected components in G, where two values are connected if they appear consecutively in the linked list.
Example 1:
Input:
head: 0->1->2->3
G = [0, 1, 3]
Output: 2
Explanation:
0 and 1 are connected, so [0, 1] and [3] are the two connected components.
Example 2:
Input:
head: 0->1->2->3->4
G = [0, 3, 1, 4]
Output: 2
Explanation:
0 and 1 are connected, 3 and 4 are connected, so [0, 1] and [3, 4] are the two connected components.
6.2 Solution with HashSet
public int numComponents(ListNode head, int[] G) {
Set<Integer> set = new HashSet<>();
for (int g : G) {
set.add(g);
}
int ans = 0;
while (head != null) {
if (set.contains(head.val) && (head.next == null || !set.contains(head.next.val))) {
ans++;
}
head = head.next;
}
return ans;
}
6.3 Solution With Union Find
public int numComponents(ListNode head, int[] G) {
DSU dsu = new DSU(G);
while (head != null && head.next != null) {
dsu.union(head.val, head.next.val);
head = head.next;
}
return dsu.count;
}
public class DSU {
Map<Integer, Integer> map; // <child, parent>, use map instead of array
int count; // the number of component groups
public DSU(int[] nodes) {
map = new HashMap<>();
for (int node : nodes) {
map.put(node, node);
}
count = nodes.length;
}
public int find(int i) {
while (map.get(i) != i) {
map.put(i, map.get(map.get(i)));
i = map.get(i);
}
return map.get(i);
}
public void union(int i, int j) {
if (map.containsKey(i) && map.containsKey(j)) {
int p1 = find(i);
int p2 = find(j);
map.put(p1, p2);
count--;
}
}
}
7. Redundant Connection
7.1 Description
In this problem, a tree is an undirected graph that is connected and has no cycles.
The given input is a graph that started as a tree with N nodes (with distinct values 1, 2, …, N), with one additional edge added. The added edge has two different vertices chosen from 1 to N, and was not an edge that already existed.
The resulting graph is given as a 2D-array of edges. Each element of edges is a pair [u, v] with u < v, that represents an undirected edge connecting nodes u and v.
Return an edge that can be removed so that the resulting graph is a tree of N nodes. If there are multiple answers, return the answer that occurs last in the given 2D-array. The answer edge [u, v] should be in the same format, with u < v.
Example 1:
Input: [[1,2], [1,3], [2,3]]
Output: [2,3]
Explanation: The given undirected graph will be like this:
1
/ \
2 - 3
Example 2:
Input: [[1,2], [2,3], [3,4], [1,4], [1,5]]
Output: [1,4]
Explanation: The given undirected graph will be like this:
5 - 1 - 2
| |
4 - 3
7.2 Solution with Graph + DFS
Construct graph with the given edges. During the construction, use DFS to search the target edge.
public int[] findRedundantConnection(int[][] edges) {
Map<Integer, List<Integer>> map = new HashMap<>();
for (int[] edge : edges) {
if (!map.containsKey(edge[0])) {
map.put(edge[0], new ArrayList<Integer>());
}
if (!map.containsKey(edge[1])) {
map.put(edge[1], new ArrayList<Integer>());
}
Set<Integer> visited = new HashSet<>();
if (dfs(map, edge[0], edge[1], visited)) {
return edge;
}
map.get(edge[0]).add(edge[1]);
map.get(edge[1]).add(edge[0]);
}
return new int[]{0,0};
}
private boolean dfs(Map<Integer, List<Integer>> map, int start, int target, Set<Integer> visited) {
if (start == target) {
return true;
}
visited.add(start);
if (!map.containsKey(start) || !map.containsKey(target)) {
return false;
}
for (int nei : map.get(start)) {
if (visited.contains(nei)) {
continue;
}
if (dfs(map, nei, target, visited)) {
return true;
}
}
return false;
}
7.3 Solution with Union Find
Create parents array, go through each edge, find and union them until find the target edge.
public int[] findRedundantConnection(int[][] edges) {
int[] parents = new int[edges.length + 1];
for (int i = 0; i < parents.length; i++) {
parents[i] = i;
}
for (int[] edge : edges) {
int u = edge[0];
int v = edge[1];
int pu = find(u, parents);
int pv = find(v, parents);
if (pu == pv) {
return edge;
}
parents[pv] = pu;
}
return new int[] {0,0};
}
private int find(int curr, int[] parents) {
while (parents[curr] != curr) {
parents[curr] = parents[parents[curr]];
curr = parents[curr];
}
return curr;
}
7.4 Solution With Union Find Template
class DSU {
int[] rank;
int[] parent;
public DSU(int size) {
parent = new int[size];
for (int i = 0; i < size; i++) {
parent[i] = i;
}
rank = new int[size];
}
public int find(int i) {
while (parent[i] != i) {
parent[i] = parent[parent[i]];
i = parent[i];
}
return parent[i];
}
public boolean union(int i, int j) {
int p1 = find(i);
int p2 = find(j);
if (p1 == p2) { // found
return false;
} else if (rank[p1] < rank[p2]) {
parent[p1] = p2;
} else if (rank[p1] > rank[p1]) {
parent[p2] = p1;
} else {
parent[p2] = p1;
rank[p1]++;
}
return true;
}
}
public int[] findRedundantConnection(int[][] edges) {
DSU dsu = new DSU(edges.length + 1);
for (int[] edge: edges) {
if (!dsu.union(edge[0], edge[1])) {
return edge;
}
}
return new int[] {0,0};
}
8. Classic Problems
- LeetCode 547 - Friend Circles
- LeetCode 817 - Linked List Components
- LeetCode 684 - Redundant Connection
- LeetCode 200 - Number of Islands
- LeetCode 305 - Number of Islands II
- LeetCode 323 - Number of Connected Components in an Undirected Graph